2010年9月10日
独立行政法人 理化学研究所
鹿(しし)おどしの原理で神経細胞が入力信号を高速演算
-神経細胞間コミュニケーションは微小信号の高速演算・威力増強へ最適化-
ポイント
- 神経細胞は、膨大なシナプスの入力信号の情報を定説以上の高速で処理
- 個々の神経細胞は、入力信号が微小であっても複雑な演算を行う能力を持つ
- 脳は、非協調的な信号が協調する大きなメカニズムで働く可能性も
要旨
独立行政法人理化学研究所(野依良治理事長)は、脳内の情報処理の単位である神経細胞が、微量の電気信号を使って互いに情報をやり取りしている情報処理のメカニズムを、数理的に説明する新たな神経計算理論を提唱しました。これは、理研脳科学総合研究センター(利根川進センター長)計算神経物理学研究チームのマーカス・ディースマン チームリーダーとモーリッツ・ヘイリアス研究員およびドイツ・フライベルクのベルンシュタイン神経計算センター機能的神経回路グループのモーリス・ダガー研究員、シュテファン・ロッター博士との共同研究による成果です。
研究グループは、生体脳に似せた人工神経回路網をコンピュータ上で再現し、神経細胞が行う情報処理のメカニズムを研究することができる、現時点で世界最高精度の手法を開発しました。新手法は、「無限の入力があると個々の入力は無視できるほど小さい効果を持つ」と仮定する、物理学では王道のアプローチを拡張した新たな理論に基づいています。神経細胞では、個々の入力は非常に小さいにもかかわらず、いくつかの入力が短時間のうちに神経細胞に到達し出力信号を発します。従来の理論では、小さい入力の単純な加算が出力を決定すると考えられていましたが、研究グループは、最後の入力は小さくとも決定的な役割を果たすため、乗算のような複雑な演算が行われていると考えました。研究グループが新たに提唱したこの神経計算理論は、神経細胞の微量な入力信号の効果を無視しないで利用することができるという特徴を持ちます。この新手法を活用して得た観測結果は、思いがけないことに、脳内での情報処理は、これまで考えられていたよりもずっと高速で行われており、個別の神経細胞が従来の理論で示されていたような入力信号の加算だけでなく、乗算のような非線形演算※1も行っていることを見いだしました。また、なぜ神経細胞が同時並行で多くのことをできるかという謎に数理的に答えを出し、何千何万もの互いに関係のない信号が互いから利を得るという「非協調的な協調」に基づく一般的なメカニズムの存在を発見しました。
本研究成果は、米国のオンライン科学雑誌『PloS Computational Biology』(9月9日付け:日本時間9月10日)に掲載されます。
背景
神経細胞は、活動電位と呼ばれる短い電気信号によって互いに情報を交換しています。活動電位が相手の神経細胞上のシナプスと呼ばれる接点に到達すると、信号を受けた細胞の電位が少しだけ変化してシナプス後電位となります。この小さな電位変化を繰り返して、シナプス後電位がある閾値に到達すると、信号を受けた神経細胞で次の神経細胞へ送る活動電位が生じます。そして、どのように神経細胞が入力を出力へ転送するのか、いつ、どの基本演算を実行するかを決めていきます。神経細胞は、何千(ヒトだと何万)ものシナプスで一見互いに関係していない小さな入力を受けており、既存の理論では、全部のシナプスの効果が単純な加算によって決定され、神経細胞そのものも入力を効率よく加算すると考えられていました。しかし、情報処理の基本単位が小さな入力を加算することだけならば、脳の複雑な機能は入力の大きさだけに依存するということになり、実際の神経活動を説明できません。そこで、研究グループは、神経細胞が小さな入力に対して乗算のような複雑な演算を行っているかどうかを理論的に証明することに挑戦しました。
研究手法と成果
理研の計算神経物理学研究チームは、神経回路網をシミュレーションする手法を開発しており、2010年、高い時間精度で神経細胞の相互作用をシミュレーションする手法の確立に成功しました。研究チームはドイツ・フライベルクのベルンシュタイン神経計算センターの研究者らとともに、神経回路の正確性を保つにはどれだけ高い機能を持つコンピュータが必要かを報告しており(Front. Neuroinform. 4:113)、そのシミュレーションソフトウェアをNEST Initiative(英語)から無料で公開しています。こうしたソフトウェア開発は、今日の理論研究に欠かせないものとなっています。この高度に領域横断的な分野の研究では、基礎的な数学の理論とともに、神経生物学や情報科学、理論物理学の力量が求められます。
研究グループは、こうした成果を基に、1秒間で何千もの入力を受けるような神経回路網に埋め込まれた神経細胞の振る舞いを数学的に記述する新しい理論を提唱しました。神経細胞を鹿おどしに例え(図1A)、シナプスへの小さな入力を絶え間なく降り注ぐ雨粒になぞらえると、鹿おどしが満杯になって重みで傾き音を鳴らす動作は、神経細胞に入ってきた入力が閾値を越え活動電位が生じる現象に相当します。これまでの理論では、水たまりの状態では1滴1滴の雨粒の効果が無くなると考え、全部の雨粒をまとめて解析していました。
今回、研究グループは、1粒1粒の雨粒の力を考慮に入れた理論を考えました。この理論は、鹿おどしが作動するきっかけとなる最後の雨粒が落ちる時間、すなわち活動電位が生じる際の最後のシナプス入力を説明しています。鹿おどしが満杯になって音を鳴らす直前には、雨粒たった1粒でも十分に威力を発揮する、すなわち、神経細胞のシナプス後電位が閾値に近づいている状況では、最後のシナプス入力が活動電位を起こすという点に注目しました。専門的には、この理論はいわゆるフォッカー・プランク(Fokker-Planck)理論※2の延長です。雨の中の鹿おどしの例えで示すように、この理論自体は一般的であるため、神経科学に限らず自然科学のさまざまな問題に使うことができると期待されています。
神経細胞の集団に同時に2つのシナプス入力がある場合を考えると、神経細胞の応答は1つずつの入力の効果を単に出力することにはなりません。鹿おどしが傾くまでにあと水滴2滴分足りない状態は、どちらか一方の入力から落下する1滴だけだと傾く量にはまだ足りず、両方の入力から1滴ずつ落下した場合にだけ鹿おどしは即座に傾きます。水滴2滴のうちどちらか1滴が落ちる条件を1、落ちない条件を0とすると、1滴だけ落ちる条件では1×(かける)0 = 0×1 = 0 となり鹿おどしは傾かず、2滴とも落ちる条件では1×1 = 1なので鹿おどしは傾くため、この瞬間だけ乗算が行われていることになります(図1B)。まさにこの鹿おどしと同じメカニズムが神経細胞で起きており、同時に2つ以上の入力が入った時だけ乗算を行い、信号を出力します。この新理論を応用すると、神経細胞集団が情報処理にほとんど時間をかけずに、入力に対して瞬時に応答するシミュレーション上の観測結果を説明することができるようになります。乗算は脳の計算の必須要素として、ある種の素早い意思決定機構を支えています。
研究グループは、加算成分を上回るような強力な乗算成分を、脳がどのように抽出しているのかも検討し、神経細胞の電位を下げるシナプス入力「シナプス抑制」を使っていることを明らかにしました。鹿おどしが雨の中に2つ存在している場合を考えてみましょう。このとき、初めの鹿おどしの竹の筒に虫が停まっている状態で、雨粒が2個目の鹿おどしに落下したとします。すると停まっていた虫は驚いて飛び去り水滴を1滴持っていくとします。つまり1個目の鹿おどしは水1滴分を失い、それと同時に2個目の鹿おどしは水1滴分を得ています。この水滴分だけ2個目の鹿おどしに比べて1個目の鹿おどしが傾く時間は余計にかかります。ふつうは鹿おどしに水滴が足されたのか虫が水滴を取り除いたのかは外からは判断できず、鹿おどしを傾けることもありません。しかし、鹿おどしがほぼ満杯の状況では、この2つの鹿おどしの間に決定的な違いが起きます。たった1滴の水が鹿おどしを傾けて空にすることもあるし、1滴失われればそれ自体はごく少量でも水面を変化させて傾かないように留まらせることができます。
神経細胞に話を戻して考えると、1個目の神経細胞を狙った抑制性の入力が2個目の神経細胞の応答を加算したものをちょうど打ち消してしまうような負の応答を起こします。こうした場合には、両方の集団を足し合わせて残るものは単なる乗算の素早い成分と、互いに打ち消し合う加算成分となります(図2)。
しかし、1つの神経細胞は、単に2つのシナプスからやってくる入力を乗算するのではなく、何千(ヒトだと何万)ものシナプス入力を乗算しています。そのため、神経細胞がこれら全部のシナプスから入力を受けた際の情報処理に耐えられるかどうかは興味深い問題です。研究グループは、同時並行で無関係の入力が相当量入っている場合には、新しく見つけた弱い入力に対する乗算応答がむしろ強まることを発見しました(図3)。これは確率的応答と呼ばれる現象で、加算成分だけで知られていましたが、新たな理論から乗算、加算どちらの場合でも見られることが分かりました。ちょうど、空っぽの鹿おどしに雨粒1滴が入っても傾かないのに対し、夏のゲリラ豪雨の雨粒なら一瞬で傾けることができるように、単独のシナプス入力だけでは神経細胞に活動電位を起こすことができませんが、たとえ個々の入力が完全にばらばら(非協調的)であったとしても、すべての入力を協調させることで、活動電位を起こすことができるようになります。これは神経細胞が同時にたくさんの演算を行うのに特化していることを意味しています。
今後の展望
本研究で調べた神経回路網は、信号が神経細胞集団に入力したあと出力する、情報が一方向に流れていくフィードフォワード構造をしています。しかし、脳は周回回路網といって、情報の流れを追いかけてみると常にどれかの神経細胞から次の神経細胞へと情報が処理されていき、また元の場所に戻ってくるような構造をしています。研究グループは特に、この周回回路網において2つ以上の神経細胞が協調して活動電位を起こす「相関活動」に興味を持っています。この協調は、神経細胞同士が互いにどう影響を与えるかに依存します。今回の研究では、1つの神経細胞が1秒以内の早い応答を引き起こすことができ、このため複数の神経細胞が短時間のうちに続けて活動電位を起こすことが分かりました。研究グループは現在、神経細胞が直接は影響を与えないが周回回路を経由して影響を与えるような状況で何が起きているかを調べています。「学習」は神経細胞同士が同期して発火することに依存しているとされています。研究グループは今後、早い乗算応答と、学習中に協調せずにバラバラに入るシナプス入力の協調に焦点を絞って研究していきます。
研究グループは、文部科学省の次世代スーパーコンピュータプロジェクトに参加しており、神戸に建設中のスーパーコンピュータ「京」で大規模神経回路モデルの探索が実現すると期待されます。脳の並列情報処理を理解することは、将来、より強力で効率のよいコンピュータを構築することができると注目されています。
発表者
理化学研究所
脳科学総合研究センター 計算神経物理学研究チーム
チームリーダー Markus Diesmann(マーカス・ディースマン)
研究員 Moritz Helias(モーリッツ・ヘイリアス)
Tel: 048-467-9644 / Fax: 048-467-9670
お問い合わせ先
脳科学研究推進部企画課Tel: 048-467-9757 / Fax: 048-462-4914
報道担当
理化学研究所 広報室 報道担当Tel: 048-467-9272 / Fax: 048-462-4715
補足説明
- 1.非線形演算
原因と結果の間に重ね合わせの関係が成り立たない関係を指す。 - 2.フォッカー・プランク(Fokker-Planck)理論
特定の状況(電位や水面のレベル)で観測しているシステム(神経細胞や鹿おどし)の反応(=出力)確率が、時間とともにどう変化するかを記述する理論。
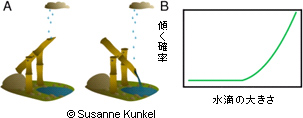
図1 雨の中の鹿おどし
鹿おどしは神経細胞の動作原理を説明する上で素晴らしいモデルとなる。
A. 雨粒はシナプスを介した入力に対応し、1粒1粒はわずかに水面を上昇させる。最後の1滴が落ちると、鹿おどしは傾いて水を排出し、戻って石を打つ。この最後の1滴は神経細胞が活動電位を起こすのに対応する。つまり、何千何万のシナプス入力がある中で、たった1つのシナプス入力が神経細胞の状態に大きな影響を及ぼすことを意味する。既存の理論では、この閾値での振る舞いを無視してきたが、今回新しく創出した理論では、まさにこの微小な入力が大きな変化をもたらす要素を考慮に入れることができた。
B. 鹿おどしの傾き(神経細胞の応答)に与える1滴の効果。応答が起きる確率は水滴の大きさの二次方程式で記述できる。つまり、ある程度の雨粒がたまった状態では、例えば2倍の大きさの水滴が落ちたら鹿おどしが傾く確率は4倍になる。これは非線形と呼ばれ神経細胞が乗算を行うことを示している。
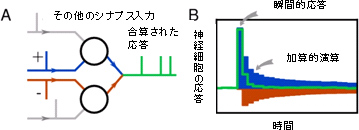
図2 抑制性入力によって起きる神経細胞の瞬間的な非加算的応答の取り出し
A. 丸は神経細胞を示す。上の神経細胞は興奮性の入力(正のシナプス入力)を受ける(青で表示)。下の神経細胞は抑制性の入力(負のシナプス入力)を受ける(赤で表示)。正の入力は鹿おどしに水が1滴足されることに相当し、負の入力は1滴失うことに相当する。そのほかの入力はバラバラと互いに無関係に入っている(灰色で表示)。
B. シミュレーション結果。上の神経細胞が活動電位を起こす直前である時(鹿おどしが傾く直前の時)、入力と出力(この場合は活動電位)はほぼ同時に起きるため、上の神経細胞は加算成分によって次の活動電位までの時間は短くなる(青の棒グラフ)。一方、下の神経細胞は負の応答を起こし、次の活動電位を起こすまでの時間は長くなる(赤の棒グラフ)。合わせると、素早い応答成分だけが残ることが分かる(緑の線)。
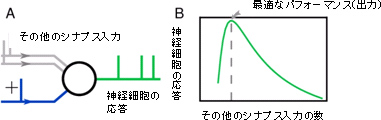
図3 神経細胞のシナプス間の「非協調的な協調活動」
A. 1つの神経細胞は、ほかの神経細胞から数千ものシナプス入力を受け取っている。神経細胞の素早い応答における1つのシナプス入力(青)の効果は、いくつの非協調的な入力を神経細胞が受けているかに依存する。
B. シミュレーション結果。神経細胞の応答が最大になるような入力の数。入力1つでは活動電位を起こせない(空の鹿おどしは1滴では傾かない)が、神経細胞は同時にたくさんの入力を受けるため、実はシナプス自体は非強調的であっても、神経細胞への働きかけでは協調し、神経細胞が同時に大量の計算を行っていればいるほどうまく働く。
