2014年8月18日
独立行政法人理化学研究所
国立大学法人東京大学
国立大学法人東北大学
異常量子ホール効果の量子化則を実験的に検証
-トポロジカル絶縁体を用いた省電力素子の基礎原理確立へ-
ポイント
- 無磁場でエネルギー損失なく電流が流れる「異常量子ホール効果」を観測
- 「異常量子ホール効果」の量子化則が「整数量子ホール効果」と同様であることを発見
- 磁場を必要としない省電力素子の実現に向け大きく前進
要旨
理化学研究所(理研、野依良治理事長)と、東京大学(濱田純一総長)、東北大学(里見進総長)は、新物質のトポロジカル絶縁体[1][(Bi1-xSbx)2Te3]薄膜に磁性元素のクロム(Cr)を添加することで、無磁場でエネルギー損失なく電流が流れる「異常量子ホール効果[2]」の量子化則[3]を観測し、異常量子ホール効果と「整数量子ホール効果[4]」が本質的に同じであることを初めて実証しました。これは、理研創発物性科学研究センター(十倉好紀センター長)強相関物性研究グループのチェケルスキー・ジョセフ客員研究員(マサチューセッツ工科大学准教授)、吉見龍太郎研修生(東京大学大学院工学系研究科博士課程)、十倉好紀グループディレクター(東京大学大学院工学系研究科教授)、強相関界面研究グループの川﨑雅司グループディレクター(東京大学大学院工学系研究科教授)、東北大学金属材料研究所の塚﨑敦教授(理研客員研究員)らによる共同研究グループの成果です。
共同研究グループは、トポロジカル絶縁体に磁性元素のクロム(Cr)を添加させた磁性トポロジカル絶縁体[Cr0.22(Bi0.2Sb0.8)1.78Te3]薄膜を基板上に作製しました。さらに、試料内部の電子数を連続的に変化させるため、電界効果型トランジスタ[5]構造としました。そこで、試料内部の電子数を少しずつ変化させながらホール抵抗を測定したところ、ホール抵抗が量子化抵抗値[6](約25.8kΩ=h/e2)で一定となり、試料が異常量子ホール状態になっていることを確認しました。さらに、制御電圧や温度依存性を詳細に調べることで、自発磁化が磁場の代わりとなることで外部磁場なく誘起される異常量子ホール効果の縦伝導度と横伝導度[7]に関する量子化則が、外部磁場で誘起される整数量子ホール効果と同様の振る舞いを示すことから、両ホール効果が本質的に同じであることを見いだしました。これにより、異常量子ホール効果についての理解が進み、無磁場でエッジ電流[8]を利用した省電力素子の実現へ大きく前進しました。
本研究は、最先端研究開発支援プログラム(FIRST)課題名「強相関量子科学」の事業の一環として行われ、成果は、英国の科学雑誌『Nature Physics』(9月号)に掲載されるに先立ち、オンライン版(8月17日付け:日本時間8月18日)に掲載されます。
背景
半導体積層構造に強い磁場をかけると、試料の端にエネルギー損失なく電流(エッジ電流)が流れます。この現象は「整数量子ホール効果」と呼ばれ、エネルギー損失がないことから低消費電力デバイスへの応用の可能性が考えられています。しかし、量子ホール効果には強い磁場が必要という欠点があります。
近年発見された「トポロジカル絶縁体」は、内部が絶縁状態でその表面が金属状態を示す物質です。表面の金属状態では、従来の半導体中での電気の流れに比べて、不純物の影響を受けずに電気を流すことができる、という特別な性質を持っています。これに磁性元素を添加した「磁性トポロジカル絶縁体」は、物質内部に磁化を持つ強磁性体にもなります。この特殊な金属状態と強磁性との関わりによって、無磁場での「異常量子ホール効果」が現れます。この現象は、自発磁化が磁場の代わりとなることで外部磁場なくエッジ電流を発生できることから整数量子ホール効果とは区別して「異常量子ホール効果」と呼ばれています。異常量子ホール効果では、無磁場でエッジ電流が発生し、物質内部の磁化の向きが反転することでエッジ電流の向きも反転するため、整数量子ホール効果に比べて、磁化を反転するだけの小さなエネルギーでエッジ電流を制御できるという利点があります(図1)。異常量子ホール効果と整数量子ホール効果は似た現象ですが、両者の関連性は今まで実験的に検証されたことがありませんでした。
研究手法と成果
共同研究グループは、トポロジカル絶縁体の1つ[(Bi1-xSbx)2Te3](Bi:ビスマス、Sb:アンチモン、Te:テルル)薄膜に磁性元素のクロム(Cr)を添加した磁性トポロジカル絶縁体[Cr0.22(Bi0.2Sb0.8)1.78Te3]薄膜を、半導体材料のインジウムリン(InP)基板上に作製しました。その上に絶縁体酸化膜と電極材料を取り付けて、電界効果型トランジスタ構造としました(図2(a)、(b))。電界効果型トランジスタ構造にすることで、外部からの制御電圧を用いて、試料内部の電子数を連続的に変化させることができます。
共同研究グループは、一定の磁場(14テスラ)下で制御電圧を変化させながらホール抵抗を測定しました(図2(c))。その結果、ある範囲の制御電圧領域でホール抵抗が量子化抵抗値(約25.8kΩ=h/e2)で一定となりました。この量子化抵抗が一定値を示すことは、[Cr0.22(Bi0.2Sb0.8)1.78Te3]薄膜が異常量子ホール状態になっていることを表しています。
次に、一定の制御電圧をかけた状態で、磁場を変化させながらホール抵抗を測定しました(図1左図)。その結果、0.3テスラの磁場をかけたときにホール抵抗の正負が反転し、ホール抵抗値が±h/e2の2つの値をとることを観測しました。これは、物質内の磁化の向きが反転することで、エッジ電流の向きも逆になったことになります。また、無磁場で生じているエッジ電流の向きを切り替えるのに必要な磁場は、わずか0.3テスラであることが分かりました。
さらに、異常量子ホール状態となっている制御電圧において、縦伝導度と横伝導度の温度依存性を測定して、整数量子ホール効果の知見を用いて見出された計算値と比較しました(図3)。図3(a)の黒線で示されるような流線やドーム状に添って縦伝導度と横伝導度は変化することが理論的な計算値で示されています。[Cr0.22(Bi0.2Sb0.8)1.78Te3]薄膜を用いて実験的に温度依存性を測定して、さまざまな制御電圧のときの結果を図3(b)に表示して検証したところ、高温から低温への変化によってどのように量子化するかが分かりました。磁場下で発生する整数量子ホール効果では、横伝導度が0.5e2/hの直線上(黒太線)で2つに分岐する軌跡(矢印に添う)を描くことが知られていました(図3(a))。図3(a)と(b)を比較すると、今回測定した異常量子ホール状態でも計算値と同様の振る舞いをすることが明らかになりました。このことから、異常量子ホール状態と整数量子ホール状態は同様の量子化則で理解できると結論しました。
今後の期待
今回の成果により整数量子ホール効果と異常量子ホール効果は本質的に同様の現象であることが示され、整数量子ホール効果の今までの知見を「無磁場」での異常量子ホール効果へ生かすことが可能になります。具体的には、エッジ電流の物理や関連する素子化技術、制御手法などの活用によって、異常量子ホール状態の素子特性の発展が期待できます。
また、自発磁化によってエッジ電流を発生できる異常量子ホール効果の実験的検証と微小磁場でのホール抵抗の符号反転を観測できたことから、今後、エッジ電流を用いた論理回路の構成に向け、制御方法の確立や実現温度の向上などを図ることで、エネルギー消費の少ないエレクトロニクス実現に寄与する可能性があります。
原論文情報
- J. G. Checkelsky, R. Yoshimi, A. Tsukazaki, K. S. Takahashi, Y. Kozuka, J. Falson, M. Kawasaki and Y. Tokura.
"Trajectory of the anomalous Hall effect towards the quantized state in a ferromagnetic topological insulator".
Nature Physics, 2014, doi:10.1038/NPHYS3053
発表者
理化学研究所
創発物性科学研究センター 強相関物理部門 強相関界面研究グループ
グループディレクター 川﨑 雅司 (かわさき まさし)
国立大学法人東京大学大学院工学系研究科
附属量子相エレクトロニクス研究センター
報道担当
独立行政法人理化学研究所 広報室 報道担当
Tel: 048-467-9272 / Fax: 048-462-4715
国立大学法人東京大学大学院工学系研究科
広報室 永合 由美子
Tel: 03-5841-1790 / Fax: 03-5841-0529
kouhou [at] pr.t.u-tokyo.ac.jp([at]は@に置き換えてください。)
国立大学法人東北大学 金属材料研究所
総務課総務係 水戸 圭介
Tel: 022-215-2181 / Fax: 022-215-2184
imr-som [at] imr.tohoku.ac.jp([at]は@に置き換えてください。)
補足説明
- 1.トポロジカル絶縁体
近年発見された物質で、物質内部が絶縁体である一方、物質表面だけは金属であるという性質を持つ。今回の研究では、トポロジカル絶縁体としての性質を持つことが知られているBi2Te3とSb2Te3という2つの物質の混合物に、磁性元素としてクロムを添加した「磁性トポロジカル絶縁体」を用いた。 - 2.異常量子ホール効果
磁場中を電子などの荷電粒子が動くと、ローレンツ力により荷電粒子の動きが曲げられる。固体物質ではこの現象をホール効果と呼び、電流にも磁場にも垂直な方向に発生する電圧をホール起電圧やホール抵抗と定義して、この値を用いることで物質内部の電荷密度などを知ることができる。物質が磁性体の場合、磁性体自身が持っている磁化が外部磁場の代わりになることで無磁場でもホール効果が発生する。この現象を異常ホール効果と呼ぶ。また、異常ホール効果によって生じる抵抗が量子化抵抗値に等しくなる現象を、異常量子ホール効果と呼ぶ。 - 3.量子化則
整数量子ホール効果や異常量子ホール効果は試料温度を十分低くした時に観測される現象で、温度が高いときはホール抵抗が量子化抵抗値に一致しない。温度を下げるに従い量子化状態へと推移していくが、このとき図3にあるような縦伝導度と横伝導度の流線的な振る舞いを量子化則と呼んでいる。 - 4.整数量子ホール効果
ホール効果によって生じる抵抗をホール抵抗と呼ぶが、ホール抵抗が量子化する現象を量子ホール効果と呼ぶ。1980年にシリコンを用いた素子で初めて報告され、現在では抵抗標準値の基準に利用されている。整数量子ホール状態では、ホール抵抗が量子化抵抗(約25.8kΩ= h/ e2)の1/2、1/3、1/4…と厳密に整数分の1になることが知られている。この時、試料の端にエネルギー損失のない「エッジ電流」が流れている。しかし、量子ホール効果は強い磁場をかけた状態でしか実現できないため、これだけでは低消費電力素子などへの応用は難しい。 - 5.電界効果型トランジスタ
半導体材料などに絶縁体材料と電極材料を取り付けた素子構造。取り付けた電極から制御電圧をかけることで、絶縁体材料を通して半導体材料中の伝導度(電荷密度)を変えることができる。制御電圧によって電流が流れる状態(オン)と流れない状態(オフ)を切り替えられるため、コンピュータの基本素子となっている。 - 6.量子化抵抗値
プランク定数 hと電気素量 eを用いて h/ e2と表される抵抗値で、約25.8kΩ。異常量子ホール状態ではホール抵抗が h/ e2に、整数量子ホール状態ではこの値の整数分の1になる。 - 7.縦伝導度と横伝導度
物質中の基本性質として、電流の流れやすさを伝導度という指標で表すことができる。磁場中ではホール効果によって電流が曲がるので、通常の伝導度(縦伝導度)と区別して、電流と垂直方向(ホール抵抗と平行)の伝導度を横伝導度と呼んでいる。通常の物質では横伝導度は小さいが、整数量子ホール効果や異常量子ホール効果では縦伝導度に比べて横伝導度が非常に大きくなることが知られている。 - 8.エッジ電流
整数量子ホール効果の試料で提案された電流のモデル。整数量子ホール状態にある試料内部では、荷電粒子がローレンツ力によって回転運動をしており、縦伝導度としては電気を流していない状態になっている。しかしながら、試料の端(エッジ)では、回転運動できずに端に添って動く荷電粒子が存在する。この端を動く荷電粒子の流す電流がエッジ電流である。
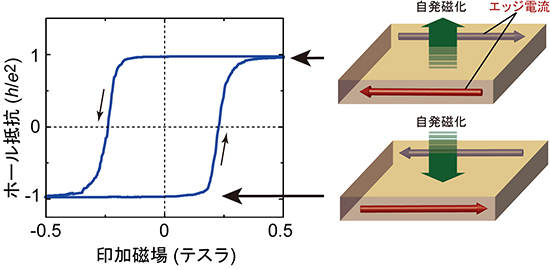
図1 異常量子ホール効果のイメージ
異常量子ホール効果では無磁場においてもエネルギー損失の無いエッジ電流が流れるため、左図のホール抵抗値が量子抵抗値となる。エッジ電流の向きは磁化の向きによって決まる。左図のように、0.3テスラでエッジ電流の向きを切り替えできる。
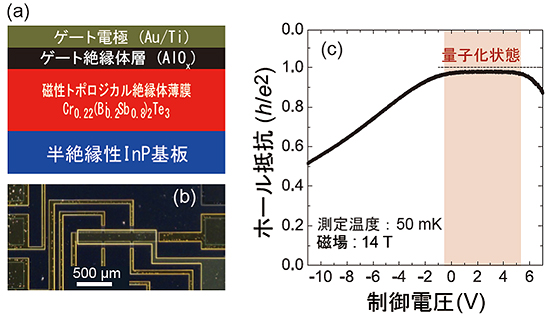
図2 電界効果型トランジスタ構造と異常量子化状態を示す電圧依存性
- (a) 磁性トポロジカル絶縁体[Cr0.22(Bi0.2Sb0.8)1.78Te3]を用いた電界効果型トランジスタ構造
- (b) 電界効果型トランジスタの光学顕微鏡写真
- (c) 制御電圧によって試料内の電子数を連続的に変化させると、ホール抵抗が量子化抵抗(約25.8kΩ)で一定となり変化しない量子化状態が観測された。
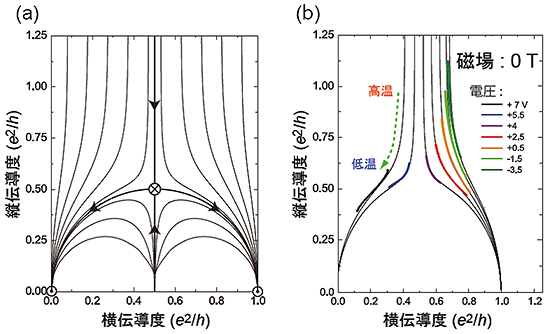
図3 整数量子ホール効果と異常量子ホール効果の縦伝導度と横伝導度の関係性
磁場下で発生する整数量子ホール効果(a)では、横伝導度が0.5e2/hの直線上(黒太線)で2つに分岐する軌跡(矢印に沿う)を描くことが計算値から知られていた。今回の実験で、異常量子ホール状態(b)でも同じ軌跡を描くことが明らかになった。このことから、異常ホール効果と整数量子ホール効果は同様の量子化則で理解できることが分かった。
