要旨

理化学研究所（理研）加藤分子物性研究室の加藤礼三主任研究員、崔亨波研究員、物質・材料研究機構若手国際研究センターの圓谷貴夫ICYS-Namiki研究員、国際ナノアーキテクト研究拠点の宮崎剛MANA主任研究者、名古屋大学大学院理学研究科の鈴村順三名誉教授らの共同研究グループは、単一成分の分子性結晶が高圧力下で「質量のないディラック電子」^[1]系となることを発見しました。

「質量のないディラック電子」系は、電子があたかも質量がないような粒子として物質中を高速に移動するため近年注目されています。例えば、グラフェン^[2]が代表的な例です。グラフェンは、線形のバンド分散^[1]が一点で交差する特異な電子状態（ディラック分散^[1]）を示します。このような電子状態を示す物質中では、電子が高速で移動することが可能なため、現在、世界中でディラック分散を持つ物質の探索が行われています。

今回、共同研究グループは、[Pd(dddt)₂]^[3]という単一の分子で構成されている結晶が圧力下で「質量のないディラック電子」系となることを明らかにしました。通常、単一成分の分子性結晶は絶縁体であり電流を流しません。[Pd(dddt)₂]の結晶も常圧では絶縁体ですが、共同研究グループは約12万気圧という高い圧力下では電流が流れるようになり、その電気抵抗が温度に依存しないことを発見しました。このような振る舞いは「質量のないディラック電子」系の特徴であることが知られています。

次に共同研究グループは、精密な第一原理計算手法^[4]により圧力下の構造と電子状態を明らかにし、高圧下でディラック分散が実現されている可能性が高いことを見つけました。さらに、モデルを使った理論解析によって、この特殊な電子状態の実現には、異なる分子層に由来するフロンティア軌道^[5]の最高占有分子軌道（HOMO^[5]）と最低非占有分子軌道（LUMO^[5]）の混成が重要な役割を果たしていることを明らかにしました。

今回、実験、計算、理論の共同研究により、通常絶縁体である単一成分の分子性結晶においても圧力をかけることによって「質量のないディラック電子」系が出現することが初めて示されました。ディラック電子系が出現する材料の範囲が広がり、新しいディラック電子系の開発が進むと期待できます。

本研究は、米国の科学雑誌『JOURNAL OF THE AMERICAN CHEMICAL SOCIETY』（1月25日号）、オンライン版（1月25日付け：日本時間1月26日）に掲載されました。

背景

ディラック電子系が示す特異な電子状態（線形分散、ゼロギャップ状態^[1]）はグラフェンや2次元層状構造を持つ有機導体α-(BEDT-TTF)₂I₃^[6]、トポロジカル絶縁体^[7]の表面状態などに現れます。固体中を高速に移動するディラック電子は電子デバイスへの応用が期待されています。そのため近年、ディラック電子系を示す物質が実験・計算の両面から探索されています。無機結晶系では色々と進展がありましたが、分子性物質については、2009年に圧力下における2次元有機導体α-(BEDT-TTF)₂I₃で実験的に確認されて以降^注1）、新しい「質量のないディラック電子」系は見つかっていませんでした。

単一の分子で構成される分子性結晶のほとんどは絶縁体で、電流は流れません。しかし、金属ジチオレン錯体^[3]と呼ばれる物質群は、結晶を構成する分子のフロンティア軌道の最高占有分子軌道（HOMO）と最低非占有分子軌道（LUMO）のエネルギー準位の差が比較的小さいことから、各フロンティア分子軌道がつくるバンドが重なることによって金属化が起こりやすいと考えられています。例えば、［Ni(tmdt)₂］^[3]というサイズの大きな（フロンティア分子軌道の拡がりが大きい）中性分子で構成される結晶では、常圧においても金属状態が実現されています。（補足説明[3]の図参照）一方、分子のサイズが比較的小さく常圧では絶縁体の性質を示す単一成分の分子性結晶であっても、高圧発生装置ダイヤモンドアンビルセル（DAC）^[8]を使うことによって、25万気圧以上の圧力における電気抵抗測定を行うことが可能となり、いくつかの単一成分の分子性結晶（例えば［Ni(hfdt)₂］^[3]）で金属状態や超伝導状態が報告されています^注2）。

また、硫化水素分子に約150万気圧という超高圧をかけると、203ケルビン（K、約-70℃）という最も高い超伝導転移温度^[9]を示す超伝導体となることが最近明らかとなり^注3）、分子性物質の圧力下での物性開拓に注目が集まっています。

注1）2009年4月30日プレスリリース「多層状単結晶で世界初の二次元ゼロギャップ電気伝導体を実現」
注2）2014年7月14日RIKEN Research「A solitary superconductor emerges under pressure（英語）」
注3）P. A. Drozdov, et al.: Nature 525（2015）73 doi:10.1038/nature14964
日本物理学会誌 2016年2月号 第71巻 第2号 清水克哉 著 最近のトピックス
「硫化水素からの高温超伝導」

研究手法と成果

共同研究グループは、単一の金属ジチオレン錯体分子[Pd(dddt)₂]で構成される分子性結晶を作製し、DACを用いた高圧下での電気抵抗測定を行いました。その結果、約12万気圧（12.6GPa）で温度に依存しない電気抵抗が現れることを見いだしました（図1）。DAC中の試料には、髪の毛の16分の1に相当する5マイクロメートル（μm、1μmは1,000分の1mm）の太さの金線4本を電極として装着しています（図2）。

圧力下の結晶構造は、実験で決定することが難しいため、高精度な第一原理計算法を用いて決定しました。その電子状態を調べた結果、線形なディラック分散を持つゼロギャップ状態を発見しました（図3）。

図1のような温度に依存しない電気抵抗は、グラフェンや分子性導体α-(BEDT-TTF)₂I₃におけるゼロギャップ状態で特徴的に見られることから、高圧下で「質量のないディラック電子状態」が実現されている可能性が極めて高いと言えます。

電子状態の理論解析の結果から、この系のディラック分散は、それぞれ異なる分子層に由来するHOMOのバンドとLUMOのバンドとから形成されることが分かりました（図3）。また、その機構は強束縛近似モデル（Tight-binding model）^[10]で説明でき、面内と面間を経由する二次摂動的なHOMOとLUMOとの混成のノード（HOMO-LUMO混成がゼロとなる点）が重要な役割を果たしていることを示しました。

今後の期待

今回、高圧下での電気抵抗測定、第一原理計算、強束縛近似モデルによる理論解析、すなわち実験・計算・理論の連携によって、高圧下の単一成分分子性結晶という予想外の物質系で「質量のないディラック電子」系が形成されていることを発見しました。ディラック電子系が出現する材料の範囲が大きく広がったことにより、今回得られた「HOMOバンドとLUMOバンドの交差」を制御するという指針をもとに、今後、分子性ディラック物質の開発が進むと期待できます。

原論文情報

• Reizo Kato, HengBo Cui, Takao Tsumuraya, Tsuyoshi Miyazaki, and Yoshikazu Suzumura, "Emergence of the Dirac Electron System in a Single-Component Molecular Conductor under High Pressure", JOURNAL OF THE AMERICAN CHEMICAL SOCIETY, doi: 10.1021/jacs.6b12187

発表者

理化学研究所
主任研究員研究室 加藤分子物性研究室
主任研究員 加藤 礼三（かとう れいぞう）
研究員 崔 亨波（さい きょうは）

物質・材料研究機構
若手国際研究センター （ICYS）
ICYS-Namiki研究員 圓谷 貴夫（つむらや たかお）
（理化学研究所　加藤分子物性研究室　客員研究員）
国際ナノアーキテクトニクス研究拠点(MANA)
MANA主任研究者 宮崎 剛（みやざき つよし）

名古屋大学 大学院理学研究科
名誉教授 鈴村 順三（すずむら よしかず）

報道担当

理化学研究所 広報室 報道担当
Tel: 048-467-9272 / Fax: 048-462-4715
お問い合わせフォーム

物質・材料研究機構 経営企画部門 広報室
Tel: 029-859-2026 / Fax: 029-859-2017
pressrelease [at] ml.nims.go.jp（※[at]は@に置き換えてください。）

名古屋大学 広報渉外課
Tel: 052-789-2016 / Fax: 052-788-6272
kouho [at] adm.nagoya-u.ac.jp（※[at]は@に置き換えてください。）

産業利用に関するお問い合わせ

理化学研究所 産業連携本部 連携推進部
お問い合わせフォーム

補足説明

• 1.ディラック電子、線形のバンド分散、ディラック分散、ゼロギャップ状態
  1928年にポール・ディラックは、相対論性理論を量子力学に組み込んだ運動方程式（ディラック方程式）を発表した。その後、グラフェン（ [2]参照）における電子の運動は、相対論的なディラック方程式と類似していることが理論的に示された。結晶中の電子のエネルギーは、電子が波として振る舞うときの波数（波長の逆数）の関数（エネルギーバンド）として表される。グラフェンの場合、二つのエネルギーバンドが一点で交差する近傍でエネルギーの分散関係（波数依存性）が線形を示す（「線形のバンド分散」という）ため、ディラック方程式を用いて記述できる。このようなバンド構造を持つ固体中の電子を、「ディラック電子」と呼ぶ。ディラック電子の質量は、電子によって満たされたエネルギーバンドと満たされていないバンドとのエネルギー差の最小値（エネルギーギャップ）に比例する。グラフェンではエネルギーギャップはゼロであり、ディラック電子は質量を持たない（「ゼロギャップ状態」）。このように電子の質量がない極限でのエネルギーバンドの分散関係は線形で円錐型（ディラックコーン）となり、「ディラック分散」と呼ぶ。ゼロギャップ状態では、電子に満たされたバンドと満たされてないバンドが、1点で接するという特殊な状況にある。
• 2.グラフェン
  グラファイトは炭素だけから成る蜂の巣状の層状物質で、鉛筆の芯として使われている。この層から１枚だけ取り出したものをグラフェンと呼び、ゼロギャップ電気伝導体として最近活発に研究されている。2010年のノーベル物理学賞は、「グラフェンに関する革新的な実験」に対してアンドレ・ガイム博士とコンスタンチン・ノボセロフ博士に与えられた。
• 3.金属ジチオレン錯体、[Pd(dddt)₂]、［Ni(tmdt)₂］、［Ni(hfdt)₂］
  

  金属-ジチオレン錯体とは、中心金属イオンに下図のような硫黄原子を含む配位子が結合した錯体のこと。一般に、配位子は孤立電子対を持つ原子の集合体（基）を持っており、孤立電子対を介して金属と配位結合して、錯体を形成する。孤立電子対とは、原子の最外殻の電子対のうち、共有結合に関与していない電子対のこと。ジチオレン錯体は、配位子全体に拡がった硫黄原子および炭素原子のpπ軌道（p電子の軌道で分子平面に対して垂直方向に延びた軌道）が結晶空間に拡がることによって金属状態を実現しやすく、分子性伝導体の材料として用いられている。単一成分分子性導体を構成する分子[Pd(dddt)₂]、［Ni(tmdt)₂］、［Ni(hfdt)₂］の構造を下記に示す。
  (dddt=5,6-dihydro-1,4-dithiin-2,3-dithiolate,tmdt=trimethylenetetrathiafulvalenedithiolate, hfdt = bis(trifluoromethyl)tetrathiafulvalenedithiolate)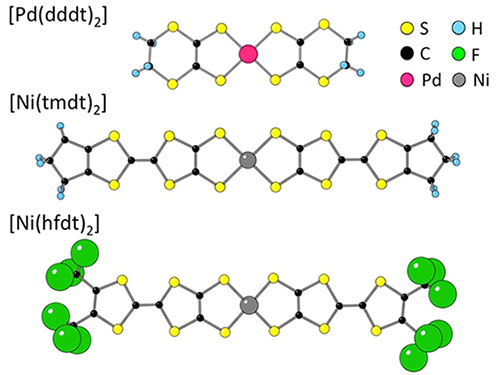

  

  金属-ジチオレン錯体を構成する分子の構造

  金属-ジチオレン錯体とは、中心金属イオンに硫黄原子（S）を含む配位子が結合した錯体のこと。上から中心金属がパラジウムの[Pd(dddt)₂]、ニッケルの[Ni(tmdt)₂]と[Ni(hfdt)₂]の構造を示す。

• 4.第一原理計算手法
  第一原理（量子力学の基本原理）に立脚して、原子の種類と位置を入力値として固体中の電子の振る舞い（電子状態/バンド構造）を計算し、物質の性質（金属、半導体、絶縁体）を調べることが可能な手法。多種多様な物質系の結晶構造と物質の性質（物理量）を、汎用性と定量性をもって精度高く求めることができる。実験結果を再現するように適宜決められるパラメータを使わないで計算を行っているため、実験と独立して物質の性質を知ることができる有効な研究手法である。実験結果が得られない未知物質や極限環境（高圧下など）での物性予測も可能である。第一原理計算は密度汎関数理論という電子系のエネルギーなどの基底状態（絶対零度）での物性を電子密度から計算することが可能であるとする理論に基づいている。この理論を提案したウォルター・コーン博士はジョン・ポープル博士とともに1998年にノーベル化学賞を受賞している。
• 5.フロンティア軌道、HOMO、LUMO
  フロンティア軌道とは、電子が占有している分子軌道のうち最もエネルギーの高い軌道を最高被占軌道（HOMO）と、占有されていない分子軌道のうち最もエネルギーの低い軌道である最低空軌道（LUMO）を指す。分子の物性や反応性において、フロンティア軌道は重要な役割を担っている。フロンティア軌道に関する理論は福井謙一博士が提唱し、1981年にロアルド・ホフマンとともにノーベル化学賞が与えられた。
• 6.α-(BEDT-TTF)₂I₃
  有機導体の一つで、有機分子BEDT-TTF（bis(ethylenedithio)tetrathiafulvalene）が並んだ層とI₃^－イオンが並んだ層とが交互に積層した層状の結晶構造をとる。I₃^－イオンは閉殻であるためにI₃^－イオン層は絶縁層である。一方、BEDT-TTF分子は+1/2価の陽イオンになって正孔ができているのでBEDT-TTF層は電流を流す。このようにして二次元電子系が形成されている。ギリシャ文字αはBEDT-TTF分子の配列の様式を表し、ほかにβ、θ、κ-型などがよく知られている。このような有機導体では、BEDT-TTF分子の配列の仕方が電子物性を決定する。β、θ、κ-型の(BEDT-TTF)₂I₃は、数Kで超伝導転移するのに対して、α型は135Kで電荷秩序による金属-絶縁体転移を起こす。この絶縁体転移は、1.5万気圧以上の圧力で完全に抑制でき、ゼロギャップのディラック電子系となる。
• 7.トポロジカル絶縁体
  物質中の電子状態のトポロジーを反映して、物質の内部（バルク）では電気を通さない絶縁体であるが、そのエッジ（2次元では端、3次元では表面）では電気を通す金属の状態が生じている特殊な物質のこと。トポロジーとは、図形のつながり具合を表す数学の概念で、長さや大きさなどの量的な関係を無視し、図形相互の位置、つながり方などを連続的に変形させても、不変な性質のこと。有名な例として、ドーナツとマグカップは同じトポロジーとして分類されるが、ボール（球）は異なる。これは、ドーナツを連続変形すれば、マグカップにできるが、ボールにするには穴を埋める必要があるからである。このような場合、トポロジカルな性質の違いは空いている穴の数で判断できる。また、メビウスの輪と普通の輪の違いは、裏表が区別できるか否かというトポロジーの違いがある。物質の性質にもこのような不変的な性質の違いが存在することが最近の物性物理学の研究で分かってきている。
• 8.ダイヤモンドアンビルセル（DAC）
  物質に高い圧力を加える装置。最も硬い物質であるダイヤモンドを加圧容器に用いることで、大がかりな設備を用いることなく、約200万気圧程度の超高圧を発生させることができる。例えば、ダイヤモンドが形成されるときの圧力は、約10万気圧である。地球を含む惑星内部の圧力環境の再現、物質合成、相転移の研究に使われている。
• 9.超伝導転移温度
  物質の電気抵抗が消失する現象（超伝導）が起こる温度。
• 10.強束縛近似モデル（Tight-binding model）
  強束縛近似とは、固体中の電子の振る舞いを計算する際に用いられる近似の一つ。結晶を構成する原子（または分子）の軌道が原子（分子）位置に束縛されている状態を出発点にして、孤立原子（分子）の波動関数の重ね合わせによって結晶中の電子の状態を記述する方法である。異なる原子または分子間の行列要素を跳び移り積分（トランスファー・インテグラル）と呼び、跳び移り積分をその近傍に限って考慮する。物質の性質を決めている重要な電子状態をうまく再現するような跳び移り積分の組み合わせのことを強束縛近似モデル（Tight-binding model）という。一般に、分子性結晶の電子状態は強束縛近似でよく記述され、興味のある物性発現の仕組みを理解するのに有効な手段となっている。