要旨
理化学研究所(理研)生命システム研究センター発生幾何研究ユニットの森下喜弘ユニットリーダーらの共同研究チーム※は、組織全体の1~数%程度の細胞の位置変化情報から、組織の発生過程における変形過程を再構築できる計算手法を開発しました。従来の発生生物学では、体内の各器官に対してその発生に必須な遺伝子、あるいは形態異常を引き起こす原因遺伝子を明らかにすることが主な課題でした。しかし、“各遺伝子が発生過程のいつ、どこで、どのように各器官の形に影響を与えるのか”を明らかにするには、発生過程で組織全体がどのように変形しているかを定量的に理解し、それを分子や細胞の動態へとつなげる必要がありますが、複雑で大きな組織をリアルタイムかつ高分解能で計測することが技術的に困難なため、ほとんど未解明でした。
そこで、共同研究チームは数理モデルを利用して、少数のラベルされた細胞あるいは細胞小集団をランドマーク(目印)とし、その位置変化情報から曲率[1]を持つ複雑なシート状組織の変形動態を再構築するための計算手法を提案しました。この手法をニワトリ胚の前脳の発生過程のデータへと応用することで、モデルの有効性を示すことに成功しました。同時に、前脳の発生過程における形態の変化(眼胞の形成と伸長)は、組織の体積変化がある領域(眼胞の先端)に集中するなど、空間的に非一様な成長によって起こるのではなく、“組織の各場所で細胞小集団が一つの軸方向につぶれることで起こること”が明らかとなりました。
こうした変形情報は、対象器官の外形変化を見るだけでは想像できません。今後は、正常胚と、先天的奇形や形態異常を引き起こす遺伝子を欠損した胚との間で、組織変形動態を定量的に比較することにより、「各遺伝子が発生過程のいつ、どこで、どのように形に影響を与えるのか」という問題を解決すると期待できます。さらに、”ヒトを含む動物の形がどのように決定されるのか”という生物学における長年の課題が解決されれば、その仕組みを応用して機能的な臓器形態のデザインや制御技術の開発へつながると期待できます。
本研究は、国際科学雑誌『Nature Communications』に掲載されるのに先立ち、オンライン版(5月2日付け:日本時間5月3日)に掲載されます。
※共同研究チーム
理化学研究所 生命システム研究センター
生命モデリングコア 計算分子設計研究グループ
発生幾何研究ユニット
ユニットリーダー 森下 喜弘(もりした よしひろ)
細胞動態計測コア
ナノバイオプローブ研究チーム
チームリーダー 神 隆(じん たかし)
背景
生物学には“ヒトを含む動物の形はどのように作られるのか”という長年未解明の問題があります。この問題は、形のデザインや制御の観点から、幹細胞の立体培養により3次元の組織を作り出す再生医学にも深く関係しています。
従来の発生生物学では分子的アプローチにより、体内の各器官に対してその発生に必須な遺伝子、あるいは形態異常を引き起こす原因遺伝子を明らかにしてきました。しかし、こうした情報の多くは、“遺伝子Xを壊すとその結果として外形が変化する”という対応関係を示すに過ぎず、実際に形が作られる物理過程の多くは分かっていません。
“各遺伝子が発生過程のいつ、どこで、どのように形に影響を与えるのか”という問題を解決するには、実際の器官発生過程で組織全体がどのように変形しているかを定量的に理解し、それを分子や細胞の動態へとつなげる必要があります。もし、器官発生過程における全細胞の軌道を一つ一つリアルタイム、かつ高分解能で計測することができれば、組織レベルの変形動態を知ることができると考えられます。しかし現状では、ショウジョウバエやゼブラフィッシュの薄くて小さな一部の組織を除いては、そうした計測は技術的に非常に難しく、断片的な情報しか利用できない場合がほとんどです。
こうした問題を解決するため、共同研究チームは、数理モデルを利用して、限られた情報から背後にある情報をうまく抽出することを試みました。
研究手法と成果
共同研究チームは、対象とする器官が十分多くの細胞から構成され、近似的に連続体とみなすことができると仮定し、“連続体の変形を記述する写像の推定”を行いました。脳や心臓など、多くの臓器の発生過程では、管や袋状の上皮組織が変形することにより目的の形が作られます。従って、特に閉曲面で近似可能、つまり2次元多様体[2]として記述可能なシート状の組織を研究対象としました(図1左)。
写像の推定の概略は、以下の通りです(図1右破線内)。
①まず、発生の各時点における対象器官の形態と、少数のラベルされた細胞あるいは細胞小集団をランドマーク(目印)として、その3次元座標を計測します。
②次に、球面調和関数[3]などを用いて、対象器官を2次元多様体としてみたときの2次元局所座標系を定義します。これは、地球表面上の各点が緯度と経度の二つの数字の組で表されるように、シート状の組織の表面上に2次元の曲線座標系が張られることを意味します。
③計測したランドマークの異なる2時点間の座標の位置情報から、写像を推定します。データ観測の確率分布と組織内部と境界の変形が滑らかであるという事前分布を組み込んだ「ベイズモデル[4]」を構築し、対数周辺尤度(ゆうど)[5]の最大化問題を数値的に解くことで、2次元座標系で表された変形写像が推定されます。
④最後に、得られた2次元写像を3次元写像に変換することで、目的の変形写像が得られます。
一旦変形写像が得られれば、各時点、各場所において、組織の体積(面積)変化速度や方向依存的な伸長や収縮などの形態変化の情報を全て計算できます。この手法を、ニワトリ胚の前脳の発生過程へ応用しました。ヒトを含む哺乳類や鳥類などの羊膜類では、脳は神経管が複雑に変形することで形成されます(図1左)。特に発生初期では、眼胞と呼ばれる突起の形成と伸長が起こります(図1左)。眼胞とは将来、その先端に眼(レンズや網膜)が形成される部位です。
推定された変形写像をもとに、組織の各点における局所的な変形量を計算しました。その結果、対象とした前脳の発生過程における形態の変化は、組織の体積変化がある領域(眼胞の先端)に集中するなど、空間的に非一様な成長によって起こるのではなく、“組織の各場所で細胞小集団が一つの軸方向につぶれることで起こる”ことが明らかになりました(図1右下)。この傾向は、発生初期から十分に眼胞が形成するまで観察されました。
観察した発生過程では、細胞の大きさや形状には大きな変化はなく、また細胞の分裂方向にも規則性がありませんでした。従って、“方向依存的な組織の変形は、細胞集団がその位置を再配列することによって実現すること”が示唆されました。すなわち図1に示した形態変化は、場所による体積変化の差を伴わずに、組織の一方向への伸長と収縮のみで起こっていました。
今後の期待
本手法により、高分解能で計測することが困難な多くの臓器に対して、全体の1~数%程度の細胞という比較的少数のランドマーク情報から、その組織変形過程を再構築することが可能になりました。また、こうした組織レベルでの解析を、正常胚と先天的奇形・形態異常を引き起こす遺伝子を欠損した胚との間で定量的に比較することで、「各遺伝子が発生過程のいつ、どこで、どのように形に影響を与えるのか」という問題を数値化することが可能になりました。
遺伝子・細胞・組織という異なる階層におけるダイナミクスの関係性が統合的に理解されることで、将来的にはヒトを含む動物の形が決定されるメカニズムの解明と、さらにはその仕組みを利用した機能的な臓器形態のデザインや制御技術へとつながることが期待できます。
本研究は、生命現象の解明に数学的なアプローチが有効であることも示しました。
原論文情報
- Yoshihiro Morishita, Ken-ichi Hironaka, Sang-Woo Lee, Takashi Jin, and Daisuke Ohtsuka, "Reconstructing 3D deformation dynamics for curved epithelial sheet morphogenesis from positional data of sparsely-labelled cells", Nature Communications
発表者
理化学研究所
生命システム研究センター 生命モデリングコア 計算分子設計研究グループ 発生幾何研究ユニット
ユニットリーダー 森下 喜弘(もりした よしひろ)
 森下 喜弘
森下 喜弘
報道担当
理化学研究所 広報室 報道担当Tel: 048-467-9272 / Fax: 048-462-4715
お問い合わせフォーム
産業利用に関するお問い合わせ
理化学研究所 産業連携本部 連携推進部お問い合わせフォーム
補足説明
- 1.曲率
曲線または曲面上の各点において、その曲線または曲面の曲がる具合を表す値。曲線は曲率が大きな点近くで急に曲がり、小さな点で緩やかに曲がる。円では、曲率は一定である。 - 2.2次元多様体
曲面を一般化した概念。構成要素の各点周りに、二つの数字の組からなる滑らかな座標系を導入することができる集合。 - 3.球面調和関数
単位球面上で定義された特殊関数。フーリエ級数展開によって任意の波形が異なる周波数を持つ三角関数の重み付き和で表されるように、異なる次数の調和関数を足し合わせることで任意の閉曲面を近似可能。 - 4.ベイズモデル
推定したいパラメータに対して、事前分布(例えば変形は滑らかに起こるなど)を仮定した統計モデル。 - 5.対数周辺尤度(ゆうど)
観測データが与えられたときの、対象とする統計モデルの周辺分布の対数をとったもの(周辺化はパラメータの積分によってなされる)。
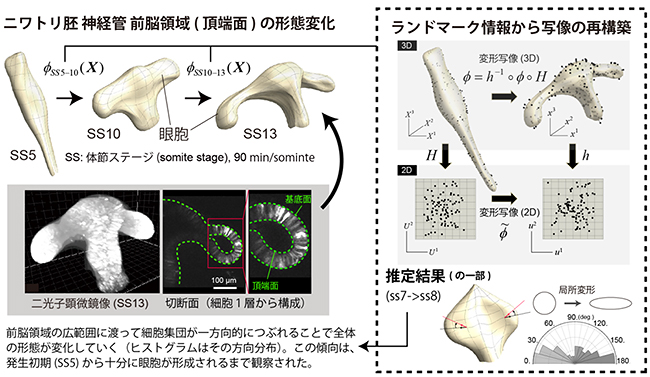
図1 曲率を持つ複雑なシート状組織の変形動態解析
左:ニワトリ胚の前脳の発生過程を示す。脳や心臓をはじめ、多くの臓器の発生過程では管や袋状の上皮組織が変形することにより最終的な形態ができあがる。
右上:本研究で提案した、限られたランドマーク位置座標情報から変形写像を推定する過程の模式図。Hとhは2次元局所座標系を与える。また、組織上の黒点は模式的なものであり、実データではない。
右下:推定された変形写像をもとに組織の各点における局所的な変形量を計算した結果、前脳初期発生における形態の変化は、組織の体積変化がある領域(眼胞の先端)に集中するなど空間的に非一様な成長が起こることで実現するのではなく、組織の各場所で細胞小集団が一つの軸方向につぶれることで実現することが明らかとなった。
