要旨
理化学研究所(理研)理論科学連携研究推進グループ 分野横断型計算科学連携研究チームの本郷優基礎科学特別研究員は、流体中に生じる「流れ」を記述する量子論的枠組みを構築し、「曲がった時空」という幾何学の言葉によって統一的に記述できることを明らかにしました。
私たちの身の回りでみられる水や空気などの物質状態は、まとめて「流体」と呼ぶことができます。この流体というものの見方は、水や空気をミクロな視点からみるのではなく、それらを構成している原子・分子を大ざっぱに眺めるというマクロな視点に立っており、「流体力学」で記述されます。一方、ミクロな視点を極限まで追究していくと、物質を構成する最小単位の素粒子で表される「量子論」で記述されるようになります。このマクロな見方とミクロな見方の関係を明らかにする研究は、20世紀初頭に物理学者ボルツマンによって始められました。そしてミクロな量子論に基づいてマクロな流体を表す理論的枠組みは、「大局的な熱平衡状態[1]」という全体として流れが生じていない状態の流体については精密に整えられました。しかし、「局所的な熱平衡状態[1]」という局所的、つまり空間の場所ごとに流れが生じている状態の流体についてはまだ確立されておらず、その理論的定式化が求められていました。
今回、本郷基礎科学特別研究員はミクロな量子論に基づいて、マクロな流体の局所的な熱平衡状態を記述する理論的定式化を試みました。その結果、局所的に流れが生じている状態を、「曲がった時空」という幾何学の言葉によって統一的に理解できることが分かりました。この記述法には、アインシュタインの一般相対性理論[2]で重力を記述するために用いられたものと同じ手法が用いられています。
本研究で構築した新しい理論的枠組みは、物質中に生じるさまざまな「流れ」について効率的かつ正確な予言を与えるものです。今後は、高エネルギー加速器衝突実験で生成されるクォーク・グルーオン・プラズマ[3]という素粒子の流体や、物性物理の研究に現れる新奇な輸送現象への応用が期待できます。
本研究は、米国の科学雑誌『Annals of Physics』に掲載されるのに先立ち、オンライン版(4月20日付け)に掲載されました。
背景
私たちの身の回りでみられる水や空気などの物質状態はまとめて「流体」と呼ぶことができます。この流体というものの見方は、水や空気をミクロな視点からみるのではなく、それらを構成している原子・分子を大ざっぱに眺めるというマクロな視点に立っており、「流体力学」で記述されます。一方、ミクロな視点を極限まで追究していくと、物質を構成する最小単位の素粒子で表される「量子論」で記述されるようになります。では、流体というマクロな見方は、量子論というミクロな見方に基づいて記述できるのでしょうか。それを実現するには、流体力学というマクロな記述と量子論というミクロな記述のギャップを埋める方法が必要となります。
ここで、流体の熱力学的な平衡状態には、「大局的な熱平衡状態」と「局所的な熱平衡状態」があります。大局的な熱平衡状態とは、流体の流れが止まり、全体としては流れが生じていない状態のことです。コーヒーにミルクを入れてかき混ぜた後、しばらくするとミルクが一様に混ざり合い、変化が起きていないようにみえる状態です。一方、局所的な熱平衡状態は、ミルクを入れたコーヒーをかき混ぜている最中のように、局所的、つまり空間の場所ごとに流れが生じている状態のことを指します。
マクロな見方とミクロな見方のギャップを埋める方法についての研究は、20世紀初頭に物理学者ボルツマンによって始められました。そして現在では、大局的な熱平衡状態にあるマクロな流体をミクロな量子論に基づいて記述する理論的枠組みは精密に整えられています。しかし、局所的な熱平衡状態についてはまだ確立されておらず、その理論的定式化が求められていました。
研究手法と成果
物質のマクロな状態を記述するには、統計集団(あるいは確率分布)と呼ばれる確率的な記述法が用いられます。流れが生じていない大局的な熱平衡状態には、温度などの熱力学的パラメータで特徴づけられる特別な確率分布の「ギブス分布[4]」が用いられます。このギブス分布により流体のマクロな状態をミクロな量子論に基づいて計算する方法は既に確立されており、「虚時間形式(松原形式)[5]の量子論」と呼ばれています。この理論的枠組みにおいて、大局的な熱平衡状態は時間方向が有限なサイズの「平らな時空上の量子論」として記述されます。
今回、本郷基礎科学特別研究員はこの理論的枠組みを、空間座標に依存する非一様な温度や流速を用いて特徴づけられる「局所ギブス分布」を導入することで、局所的に流れが生じている局所的な熱平衡状態に対して拡張できると考えました。この場合、温度や流速の非一様性のために、局所的な熱平衡状態はもはや平らな時空上の量子論では記述できなくなりますが、「曲がった時空」という幾何学の言葉で記述できることが分かりました。これは、流れを記述する方法(流体力学)と曲がった時空を記述する方法(アインシュタインの一般相対性理論)との類似性に基づいています。
一般相対性理論では、「質量を持った物体の配置」が宇宙の幾何学(曲がった時空の構造)、つまり重力を決めています(図1)。それに対して本研究では、「温度や流速の非一様性という熱的な配置」が流体中に創発する(現れる)曲がった時空の幾何学を決めています(図2)。この曲がった時空は、私たちの宇宙が一般相対性理論による効果が無視できる平らな宇宙であっても、流体を量子論的に扱おうとすると自然に現れてくるため、“局所的な熱平衡状態にある流体中では、曲がった時空が熱的に創発している”ということができます。
以上のように、流体力学というマクロな記述と量子論というミクロな記述の間のギャップを、曲がった時空という幾何学の言葉で埋められることが明らかになりました。この理論体系は実用面においても有用です。流体中には、エネルギーの流れ、運動量の流れ、電荷の流れといったさまざまな流れが生じており、通常、これらは別々の輸送現象として解析されがちです。しかし、このようなさまざまな輸送現象は、曲がった時空という幾何学の言葉を用いることで、統一的に記述できます。この「流れの統一」により、局所的な熱平衡状態にある流体中の輸送現象を、効率的かつ正確に記述するための理論的な基礎を築くことができました。
今後の期待
本研究で構築した理論を用いると、流体中で曲がった時空における量子論の効果を検証できる可能性があります。その一つが、新たな輸送現象の理論的提案です。具体的には、物質中の電子系や高エネルギー加速器による衝突実験で生じるクォーク・グルーオン・プラズマのように、温度や流速が急激に変化している流体中の「流れ」の性質を理論的に予言できると考えられます。
一方、今回、局所的な熱平衡状態にある流体中の流れを記述する理論的方法を確立しましたが、現実の流体中では厳密な局所的な熱平衡状態から微妙にずれることにより、摩擦に性質が似た散逸的な輸送現象が生じます。例えば、高温の物体から低温の物体へ熱が伝わる熱伝導などの現象が挙げられます。本研究で行った流れの統一は、非散逸的な輸送の統一という部分的なものにとどまっているため、散逸的な輸送までを含めた真の意味での流れの統一が幾何学の言葉とどのように関係するのかを明らかにするという課題が残されています。
原論文情報
- Masaru Hongo, "Path-integral formula for local thermal equilibrium", Annals of Physics, doi: 10.1016/j.aop.2017.04.004
発表者
理化学研究所
研究推進グループ 理論科学連携研究推進グループ(iTHES) 分野横断型計算科学連携研究チーム
基礎科学特別研究員 本郷 優(ほんごう まさる)
 本郷 優
本郷 優
報道担当
理化学研究所 広報室 報道担当
Tel: 048-467-9272 / Fax: 048-462-4715
お問い合わせフォーム
産業利用に関するお問い合わせ
理化学研究所 産業連携本部 連携推進部
お問い合わせフォーム
補足説明
- 1.大局的な熱平衡状態、局所的な熱平衡状態
コーヒーにミルクを入れかき混ぜてしばらく待つと、ミルクが一様に混ざってコーヒーの流れが止まる。一様に混ざったコーヒーはその後、私たちの目には変化が起きていないようにみえる。このようにマクロにみて全体に変化のない状態を大局的な熱平衡状態といい、コーヒーの温度やミルクの濃度などの数少ない物理量で表される。一方、かき混ぜている最中の状態は大局的な熱平衡状態ではなく、空間の各点でのコーヒーの温度やミルクの濃度などの物理量で記述できる。このような、全体としては大局的な熱平衡状態にはないが、局所的にみると熱平衡になっている状態を局所的な熱平衡状態という。局所的な熱平衡状態は、熱平衡状態の空間的なパッチワークで作られた状態と考えられる。 - 2.アインシュタインの一般相対性理論
物質間に働く力の一つに重力がある。二つの物質間には引力(重力)が働くというニュートンの万有引力の法則は、現在ではアインシュタインの一般相対性理論によって「時空が曲がることによって生じる幾何学的な効果」として理解されている。1915年ごろに理論的定式化がされた一般相対性理論の予言は、現在GPS(全地球測位システム)などの技術に応用されており、実験的にその正しさは多角的に検証されている。 - 3.クォーク・グルーオン・プラズマ
物質をミクロにみていくと、クォークやグルーオンなどの素粒子によって構成される。通常の環境下では、クォークやグルーオンは単体では存在せず、陽子や中性子の中に閉じ込められているが、約2兆℃という超高温下ではこれらがばらばらになった一種のプラズマ状態が実現されると考えられている。このプラズマ状態のことをクォーク・グルーオン・プラズマといい、高エネルギー加速器による衝突実験において生成される。 - 4.ギブス分布
1900年代にギブスによって、熱平衡状態を表すために導入された確率分布の一つ。ギブス分布は、温度や化学ポテンシャルという熱力学的パラメータによって熱平衡状態を特徴づける。ボルツマン分布ともいう。 - 5.虚時間形式(松原形式)
大局熱平衡状態にある量子系を記述するために、1950年代に松原武生博士らによって確立された理論形式のこと。量子力学における時間発展との類似性に基づいて、ギブス分布により記述される温度の効果を「時間発展」として捉える。このとき、実数で与えられる通常の時間とは異なり、形式的に「虚数」を時間に代入することで温度の効果が取り入れられるため、「虚時間形式」という名前が付いている。
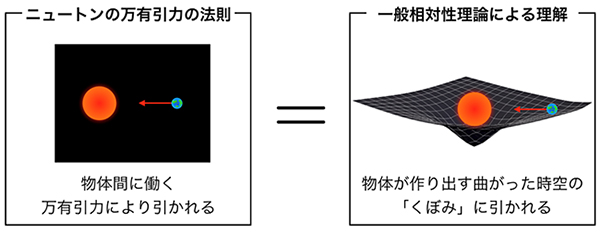
図1 アインシュタインの一般相対性理論による重力の理解
物体と物体の間には万有引力という互いに引き合う重力が働くことがニュートンにより示された(左図)。この万有引力の法則を「時間・空間(時空)が曲がる」という幾何学の言葉によって説明したのがアインシュタインの一般相対性理論である。一般相対性理論によると、物体の存在により時空が曲がることで物体の運動が歪められる。その結果、力が働いているようにみえるが、この力こそが万有引力の正体であると理解されている(右図)。
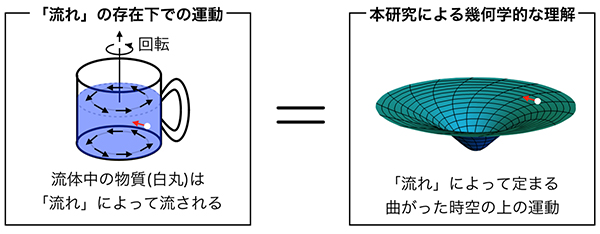
図2 「流れ」を幾何学の言葉で記述する方法の概念図
流体が流れている状況は、「流れ」によって物体の運動が曲げられる(左図)。これは、一般相対性理論において、時空の曲がり具合によって物体の運動が歪められる状況(図1)に類似していると考えられる。この類似性を用いることで、流れが存在する局所的な熱平衡状態を、「曲がった時空」を記述する幾何学的な言葉に翻訳して理解することができる(右図)。
