革新知能統合研究センター 数理科学チーム
チームリーダー 坂内 健一(D.Math.Sci)
研究概要

当チームは、幅広い純粋数学・理論物理の研究者の力を借りて、人工知能・機械学習分野における様々な数学的課題に組織的に取り組んでいます。整数論、数論幾何、代数幾何、偏微分方程式、超弦理論、量子多体系、微分幾何、位相幾何、作用素環論、確率論、統計など、幅広い数理科学・物理分野の研究者が参加して、人工知能・機械学習の専門家とともに、研究を進めています。
研究主分野
- 数学
研究テーマ
- 機械学習
主要論文
- 1.
I. Ishikawa, K. Fujii, M. Ikeda, Y. Hashimoto, Y. Kawahara.:
"Metric on nonlinear dynamical systems with Perron-Frobenius operators"
The 32nd Conference on Neural Information Processing Systems (NeurIPS2018), Montreal, Canada. - 2.
M. Ohnishi, M. Yukawa, M. Johansson, and M. Sugiyama.:
"Continuous-time Value Function Approximation in Reproducing Kernel Hilbert Spaces"
he 32nd Conference on Neural Information Processing Systems (NeurIPS2018), Montreal, Canada. - 3.K. Kobayashi, N. Hamada, A. Sannai, A. Tanaka, K. Bannai, and M. Sugiyama.:
"Bezier Simplex Fitting: Describing Pareto Fronts of Simplicial Problems with Small Samples in Multi-objective Optimization," AAAI-19, (2019). - 4.K. Hashimoto, S. Sugishita, A. Tanaka, and A. Tomiya.:
"Deep learning and the AdS/CFT correspondence"
Phys. Rev. D98 no. 4, (2018) 046019. - 5.Y. Takai.:
"Indivisibility of relative class numbers of totally imaginary quadratic extensions and vanishing of these relative Iwasawa invariants"
Journal of Number Theory 186, (2018), 162-179. - 6.K. Hashimoto, S. Sugishita, A. Tanaka, and A. Tomiya.:
"Deep Learning and Holographic QCD"
Phys. Rev. D98 no.10, (2018) 106014. - 7.
T. Kuwahara, T. Ishii, T. Mori, and N. Hatano.:
"Heating in integrable time-periodic systems"
Phys. Rev. Letters Vol 120, 220602 (2018). - 8.
M. Ikeda and M. Sobajima.:
"Life-span of solutions to semilinear wave equation with time-dependent critical damping for specially localized initial data"
Math. Ann., 372, (2018), 1017-1040. - 9.
M. Ikeda and T. Inui.:
"The sharp estimate of the lifespan for the semilinear wave equation with time-dependent damping"
Diff. Int. Equs., 32, (2019), 1-36. - 10.K. Bannai, K. Hagihara, S. Kobayashi, K. Yamada, S. Yamamoto and S. Yasuda.:
"Category of mixed plectic Hodge structures"
arXiv:1705.05522 [math.AG], to appear from the Asian Journal of Mathematics.
研究成果(プレスリリース)
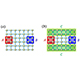
2022年4月26日
有限温度状態での量子もつれに関する普遍的性質の発見
2022年1月6日
量子もつれに劇的な変化をもたらす新たな条件の発見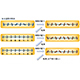
2021年5月25日
“自然界”を効率的に学習する方法を開発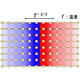
2021年3月8日
低温下における量子もつれの新法則を発見
2020年9月8日
量子もつれの境界則に対する新しいメカニズムの発見
2020年7月13日
線形光円錐問題の数学的な解決
関連リンク
メンバーリスト
主宰者
- 坂内 健一
- チームリーダー
メンバー
- 田中 章詞
- 上級研究員
- 関坂 宏子
- 上級研究員
- 池田 正弘
- 研究員
- 竹内 大智
- 基礎科学特別研究員
- 東條 広一
- 基礎科学特別研究員
- 紅村 冬大
- 基礎科学特別研究員
- 吉田 純
- 特別研究員
- KIRAL Eren Mehmet
- 客員研究員
- 小林 景
- 客員研究員
- 石川 勲
- 客員研究員
- 伊藤 哲史
- 客員研究員
- 服部 広大
- 客員研究員
- 川平 友規
- 客員研究員
- 小田 芳彰
- 客員研究員
- 佐々田 槙子
- 客員研究員
- 安田 正大
- 客員研究員
- 早野 健太
- 客員研究員
- 澤野 嘉宏
- 客員研究員
- 垣村 尚徳
- 客員研究員
- 大平 徹
- 客員研究員
- 平岡 裕章
- 客員研究員
- 太田 慎一
- 客員研究員
- 高津 飛鳥
- 客員研究員
- 山本 修司
- 客員研究員
- 坂本 龍太郎
- 客員研究員
- 福泉 麗佳
- 客員研究員
- 三内 顕義
- 客員研究員
- 後藤 有輝
- 大学院生リサーチ・アソシエイト
- 伊藤 歌那
- 大学院生リサーチ・アソシエイト
- 和知 秀忠
- 大学院生リサーチ・アソシエイト
- 渡邉 南
- 研究パートタイマーⅠ
- 金村 佳範
- 研究パートタイマーⅠ
- 中村 真緒
- 研究パートタイマーⅡ
- 小川 実里
- 研究パートタイマーⅡ
お問い合わせ先
Email: kenichi.bannai [at] riken.jp
※[at]は@に置き換えてください。
