Manifold Approximation of 3D Medial Axis
Shin Yoshizawa

-
In this research, we propose a novel approach to obtain a Voronoi-based skeletal mesh which is an approximation of the 3D medial axis. The method is based on the 2-sided manifold triangle mesh: A Skeleton-based Approach for Detection of Perceptually Salient Features on Polygonal Surfaces, Hisada, M., Belyaev, A. G. and Kunii, T. L., Computer Graphics Forum, Vol. 21, No. 4, 2002, pp. 689-700. First, a Voronoi sites are extracted by the QuickHull: The Quickhull algorithm for convex hulls, Barber, C.B., Dobkin, D.P., and Huhdanpaa, H.T, ACM trans. on Mathematical Software 22:469-483, 1996, algorithm from a given triangle mesh. Second, the inner sites are classified via a bounding box and the approximated surface normal. For each original mesh vertices, we assign the arithmetic mean of extracted Voronoi sites which form the Voronoi cell of the corresponded mesh vertex. The connectivity of the skeletal mesh is equivalent to the original mesh. Although 3D Voronoi sites are not exact approximation of the medial axis and the medial axis is not a manifold, our Voronoi-based skeletal mesh have wide possibility of practical applications because any conventional mesh processing scheme can be applied to our Voronoi-based skeletal mesh.
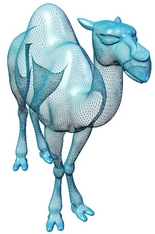



This research is collaborated with Prof. Dr. A. G. Belyaev and Prof. Dr. H.-P. Seidel. The method was used in skeleton-based mesh deformation papers ACM SM'03 and EG'07. This research was supported by Aim@Shape project.

Medial Axis
-
(*): Note that a 3D medial axis approximation is a nightmare: See theoretical analysis in prof. Amenta's works. You can not expect the correct medial axis for the Dupin's cyclides parts (spheres, cones, cylinders tori, and planes) Skeleton Degenerating Theorem: the medial axis degenerates to the point or curves in Dupin's cyclides. Also, the medial axis is very sensitive for small perturbations of the original figure/shape, see Skeleton Branching Theorem: The 2D and 3D Skeleton Branching Theorem are described in
- Visualization and Study of Dynamic 2D Shapes via Curvature, Shin Yoshizawa and Alexander G. Belyaev, Multimedia Modeling 2000, pp. 469-489, November 13-15, 2000, Nagano, Japan.
- On Evolute Cusps and Skeleton Bifurcations, Alexander G. Belyaev and Shin Yoshizawa, Shape Modeling and Applications, pp. 134-141, May 7-11, 2001, Genova, Italy.
Skeleton Degenerating Theorem
The medial axis degenerates to the point or curves in Dupin's cyclides. The proof is easy, the end points/rib of medial axis are equivalent to the focal surfaces (evolute surfaces) singularities of the original surface. The focal surfaces degenerates a point or curves if and only if e_max = e_min = 0, where e_max and e_min are the principal curvature derivatives w.r.t. their principal directions, respectively. The surfaces which satisfies the above equation is a surface family so called Dupin's cyclides.
C++ Code
-
You can download the C++ code which is TAR.GNUZIP file. After applied gunzip and tar -xf, please read README.txt and the simple manual. Questions and Bug report are welcome to my e-mail: shin.yoshizawa_At_mpi-sb.mpg.de.
Copyright
All rights are reserved by Shin Yoshizawa. This C++ source files are allowed for only primary user of research and educational purposes. Don't use secondary: copy, distribution, diversion, business purpose, and etc.. In no event shall the author be liable to any party for direct, indirect, special, incidental, or consequential damage arising out of the use of this program and source files.(*): You need qhull in order to run my program. Please establish the executable file of the qhull program in the same directory of my code. The file name should be qhull. For the Windows user, you may have qhull.exe, therefore, you have to change the line of my code in the file "Polyhedron.h", line 125 as "system("./qhull.exe < tempfile1.txt v o TO tempfile2.txt"); " instead of "system("./qhull < tempfile1.txt v o TO tempfile2.txt");".
Simple Manual
- Compile: By using attached Makefile, you may run "make". You should use the later versions of g++ 2.95.
- Execute: Run "./Skeleton input.ply2 output.ply2". Mesh data have to be constructed by the PLY2 format.
- Recall: you need qhull in the same directory of my program.
- Input (input.ply2): A 2-manifold triangle mesh.
- Output (output.ply2):A 2-manifold triangle mesh approximation of the medial axis whose vertex ID corresponds to the original vertex ID.
- Orientation (orientation):Integer: When you obtain the outer medial axis instead of the inner medial axis, you can change this value to 0 to extract opposite one. Because of the orientation consistency, sometime you will get the opposite one of the inner medial axis. If "orientation = 1" then the original orientation is chosen.
- Boundary Position (boundarymap):Integer: The Voronoi diagram approximation is unstable around the original mesh boundaries because there is no points. Therefore, I set the medial axis boundaries are equal to the original mesh boundaries in default setting. You can change this value to 0 to map the medial axis boundaries to the approximated positions instead of the original mesh boundaries.
- Bounding Box Ratio (BBOXCONSTANT):double: Sometime, the approximated Voronoi sites go far from the original mesh because of the difficulty of the Voronoi diagram calculation. This value represents a ratio of bounding box which suppress such wrong Voronoi sites. The Voronoi sites which are not inside of this bounding box are removed from candidates of medial axis vertex calculations.
How to use
Options
You can use the following options by changing the code in the constructor "Polyhedron()" of "Polyhedron.h". Also you should clean object file "make clean" then "make". The default setting is as follows:Polyhedron(){
// Default setting
orientation=1;
boundarymap=1;
BBOXCONSTANT = 1.25;
}
How can we get a better result ?
The approximation quality depends on the input mesh density and the vertex distribution. To obtain a good approximation of the Voronoi sites, it is better to use a dense uniform mesh for the input mesh. If you do not satisfy the results then I would recommend to apply the bitangential smoothing or the Loop subdivision. As described in the paper, the bitangential smoothing reduces artifacts in the result caused by irregular vertex distribution or sharp features. Also it is well-known that we have to establish a dense input mesh (r-sampling) to approximate an appropriate Voronoi sites for the medial axis approximation. The Loop subdivision helps us increasing mesh density. According to my numerical experiments, the Loop subdivisions without the limit position projection is better to keep the original shape for the medial axis approximation. Although these smoothing and subdivision change the original geometry, these pre-processing are really useful to approximate the medial axis for practical applications. It is also interesting to consider the post-processing. For instance the images represented in this page are produced by this C++ code but also I applied a special smoothing (bilaplacian smoothing projected on the normal vector direction where the inner product between the normal and smoothing vector is negative if it is positive then that skeletal mesh vertex is not moved by the smoothing.) to the extracted skeletal mesh.
Log
-
May 25, 2011: Fix a bug (initialization, no effect for UNIX/Linux) in IDList.h for the latest Windows users, thanks to Yuee Liu.
Apr. 12, 2011: Fix small memory leak in IDSet.cxx, thanks to Anuwat Dechvijankit.
Apr. 18, 2008: Move to RIKEN.
Apr. 18, 2008: Solve g++ (GCC) version 4 problem.
Jun 11 2004: Update.