Renormalization Theory
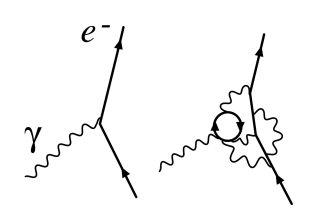 Renormalized vertex
Renormalized vertex
The mathematical technique of renormalization has its origins in the use of constants and parameters in the formulation of physical laws, which can change as a result of interaction with a particular medium or substrate. Normalization refers to the process of choosing base units for these laws such that certain physical constants, such as the speed of light, become equal to unity, making it easier to see underlying relations between dynamic variables. The term "renormalization" originated in the idea of normalizing physical laws relative to a new constant.
The field of “renormalization theory” emerged from a crisis in physics in the early 20th century, when physicists realized that this change of constants can produce infinite results in the case of quantum field theory, at the time considered to be the ultimate framework for the laws of nature at a microscopic scale. The problem was solved by a new technique (renormalization) by which the summation of an infinite number of energy levels at short distances was avoided by imposing a minimum cutoff on fields.
Shinichiro Tomonaga, a Nobel prize-winning physicist who joined RIKEN's Nishina Laboratory in 1932, played a seminal role in the development of renormalization theory. The son of a professor of philosophy at Kyoto Imperial University, Tomonaga worked on research in the area of quantum electrodynamics under the guidance of Yoshio Nishina. In 1943, he published the “super-many-time theory,” which reconciled quantum mechanics with the theory of relativity. Tomonaga further developed these ideas in his work on renormalization theory, for which he, along with Julian Schwinger and Richard Feynman, was awarded the Nobel Prize in 1965.
The new theory was key to the development of quantum electrodynamics and has become a central technique in quantum field theory. Tomonaga once reflected, “My career in physics came about because of Einstein’s visit to Japan in 1922, when I realized that the world of physics holds many wonders. I was enchanted by the possibility of investigating this fascinating world.”
