Apr. 13, 2018 Research Highlight Physics / Astronomy
Organisms may use second-order optimization when foraging
A mathematical model predicts that organisms mix both directed and random search patterns to find nourishment sooner
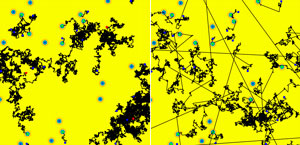 Figure 1: A second-order optimization of foraging (right) recreates the behavior of real organisms more accurately than first-order gradient-based optimization (left). Reprinted, with permission, from Ref. 1. Copyright 2018 by the American Physical Society.
Figure 1: A second-order optimization of foraging (right) recreates the behavior of real organisms more accurately than first-order gradient-based optimization (left). Reprinted, with permission, from Ref. 1. Copyright 2018 by the American Physical Society.
A classical type of random motion emerges from a model of the foraging patterns of animals and microorganisms developed by two RIKEN scientists1.
All mobile cells and organisms tend to move toward some chemicals and away from others. For example, white blood cells are attracted by inflammatory signals, while bacteria move toward higher concentrations of sugars. On a larger scale, foraging animals explore their environment to find food using their senses. At times, these movements appear to be random, whereas at other times they seem to be directed, depending on the conditions.
Scientists have observed two kinds of random movements: Brownian motion, which is the random motion that microscopic particles undergo when buffeted by molecules in a liquid or a gas, and Lévy walks, which are characterized by short steps interspersed by the occasional longer one. Researchers are still trying to understand why Lévy walks fit experimental data in so many cases.
The directed search of simpler organisms such as bacteria is often modeled as a gradient search. It is generally assumed that the organism simply follows the steepest increase in the concentration of the target chemical, which is known as first-order optimization.
The general consensus has been that different mechanisms are responsible for the directed and random search patterns. But now, Łukasz Kuśmierz and Taro Toyoizumi from the RIKEN Brain Science Institute have challenged this assumption by theoretically showing that a common mechanism can lead to both kinds of search patterns.
 Łukasz Kuśmierz (left) and Taro Toyoizumi (right) have shown that Lévy walks emerge in an organism’s movement from the second-order gradient-based optimization required to model chemotaxis. © 2018 RIKEN
Łukasz Kuśmierz (left) and Taro Toyoizumi (right) have shown that Lévy walks emerge in an organism’s movement from the second-order gradient-based optimization required to model chemotaxis. © 2018 RIKEN
They applied a simple extension to first-order optimization that adjusts the size of each step so that it is proportional to the smoothness of the variation in concentration. Brownian motion emerges from the first-order method, whereas Lévy walks naturally emerge when the extension is used in the presence of sensory noise (Fig. 1).
“We discovered that this second-order optimization process reproduces all the properties of Lévy walks when the concentration landscape is relatively smooth,” explains Toyoizumi. “This gives an appealing hypothesis as to how Lévy walks might emerge.”
The finding indicates that animals and microorganisms may be performing complex calculations, including division, while searching for food and other resources. It also suggests that adopting a second-order optimization method is a useful strategy to efficiently combine features of directed and random search patterns.
Researchers from Toyoizumi’s lab are exploring whether their findings have application to neuroscience. “We are now working on the possibility of applying these ideas to models of changes in brain synapses, known as neuroplasticity,” says Kuśmierz. “Traditional learning models assume that each learning step makes a small change along the most promising direction. We are exploring if Lévy walks facilitate faster learning in neural networks.”
Related contents
References
- 1. Kuśmierz, Ł. & Toyoizumi, T. Emergence of Lévy walks from second-order stochastic optimization. Physical Review Letters 119, 250601 (2017). doi: 10.1103/PhysRevLett.119.250601
