Apr. 19, 2019 Research Highlight Physics / Astronomy
A smaller spin system yields its phase diagram
‘Compactifying’ a system allows theorists to calculate its phase diagram
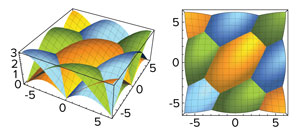 Figure 1: By compactifying a spin system with a certain symmetry, RIKEN researchers have obtained its phase diagram. Modified from Ref. 1 and licensed under CC BY 4.0 © 2019 M. Hongo et al.
Figure 1: By compactifying a spin system with a certain symmetry, RIKEN researchers have obtained its phase diagram. Modified from Ref. 1 and licensed under CC BY 4.0 © 2019 M. Hongo et al.
By employing a clever approximation, three theoretical physicists at RIKEN have calculated the phase diagram for an extension of a system proposed over 30 years ago1. In addition to advancing the theory of condensed matter physics, this finding could have practical implications for systems made up of particles with the quantum property of spin.
Back in 1983, Nobel Prize laureate Duncan Haldane caused a major stir in the fields of condensed-matter and high-energy physics. He was considering one-dimensional systems of particles of alternating up and down spins (so-called antiferromagnetic systems) and argued that systems with integer spins (such as nuclei of atoms) behave fundamentally differently from those with half-integer spins (such as electrons). This conjecture went against the received wisdom of that time, but it has since been vindicated, and it contributed to Haldane being jointly awarded the Nobel Prize in physics in 2016.
Now, Masaru Hongo and Tatsuhiro Misumi of the RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program and Yuya Tanizaki of the RIKEN BNL Research Center have analytically investigated the phase structure of a novel kind of so-called nonlinear sigma model. This model describes a special spin-chain system, which is an extension of the system proposed by Haldane.
To achieve this, the researchers had to reduce the size of the system by ‘compactifying’ it. This permitted them to use a mathematical technique known as perturbative expansion without the fear that it would explode and give excessively high values. They also employed a twisted boundary condition along the direction of compactification.
 Masaru Hongo (left), Tatsuhiro Misumi (center) and Yuya Tanizaki (right) have obtained the phase diagram of a two-dimensional nonlinear flag sigma model with respect to two variables. © 2019 RIKEN
Masaru Hongo (left), Tatsuhiro Misumi (center) and Yuya Tanizaki (right) have obtained the phase diagram of a two-dimensional nonlinear flag sigma model with respect to two variables. © 2019 RIKEN
“To calculate this kind of system quantum mechanically, you have to perform very complicated calculations, which involve a property known as the quantum coherence of the system,” explains Hongo. “If you consider a very large system, the coupling constant becomes larger and larger, which prevents us from doing analytical calculations. That’s a very big problem, but we have overcome it by properly compactifying the theory.”
The three researchers obtained a phase diagram of the system in terms of two variables (Fig. 1). They analytically checked that the generalized Haldane conjecture was true by showing that the obtained phase structure was consistent with that of a recently proposed conjecture. “This implies that the results for a twisted compactified model that is sufficiently small are smoothly connected to those for the original uncompactified model, whose analytic calculation is too difficult to perform,” says Hongo.
Hongo notes that the phase diagram could be applicable to experiments involving ultracold atomic systems that mimic spin systems. He also says that the trio intends to see if they can extend this finding to more general systems.
Related content
References
- 1. Hongo, M., Misumi, T. & Tanizaki, Y.Phase structure of the twisted SU(3)/U(1)2 flag sigma model on R x S1. Journal of High Energy Physics 2019, 70 (2019). doi: 10.1007/JHEP02(2019)070
