Oct. 5, 2018 Perspectives Biology Computing / Math
Math is the common denominator
Engaging mathematicians is the key to accelerating the impact of interdisciplinary research.
 A physicist has used math and modeling to help biologists figure out how chromosomes replicate and part ways without becoming tangled. © BIOPHOTO ASSOCIATES/SCIENCE PHOTO LIBRARY
A physicist has used math and modeling to help biologists figure out how chromosomes replicate and part ways without becoming tangled. © BIOPHOTO ASSOCIATES/SCIENCE PHOTO LIBRARY
All theoretical approaches in the natural sciences are based on mathematics, but the truth is that most researchers are still using equations developed in the first half of the 20th century or earlier. In the intervening years, mathematics has become quite abstract and hard to understand. However, with increasing insights into genomics and huge advances in imaging, it’s becoming obvious that the biological sciences have a lot to gain from newer developments in mathematical fields such as topology, algebraic geometry and stochastic analysis. Arguably, math is meeting the biosciences this century much as it met physics in the last.
As a result, math’s growing relevance is being recognized worldwide. In April, a 68-page report chaired by computational mathematician Philip Bond, called The Era of Mathematics—an Independent Review of Knowledge Exchange in the Mathematics, was launched at the House of Lords in the UK. The authors focused on how the UK can support the expanding need for mathematics. Their recommendation—tripling funding for mathematics. The reasons cited include a Deloitte analysis that suggests the benefit-to-cost ratio of using mathematical science is 588:1, which dwarfs engineering’s strong 88:1.
Linked to math’s increasing sway is its ability to act as a bridge between interdisciplinary research teams tackling big questions. Theoretical science and math are a good starting point to try to talk across disciplines. The last few decades have seen concerted, if patchy, global efforts to boost interdisciplinary study, including incentives within the US’s National Institutes of Health grants program from 2004 to 2012 and successful European Union policies on knowledge exchange. Today, at least a third of cited papers point to other disciplines. Institutions in Asia are also becoming more conscious of the benefits of multidisciplinary teams to applied and large-scale projects. For example, prominent Chinese universities have recently set up interdisciplinary departments, and, in Japan, the quite recently established Okinawa Institute of Science and Technology Graduate University was designed specifically to support this type of work. Fortunately for RIKEN, one of Japan’s most focused and long-standing interdisciplinary programs, the RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS), has already started work on integrating mathematicians into their agenda.
Mathematics brings disciplines closer together
The iTHEMS program was founded after I moved to the RIKEN Nishina Center for Accelerator-Based Science in 2012. After ten years at the University of Tokyo, I moved to RIKEN, in part because I wanted to work in a less-siloed environment. In 2013, I helped launch an interdisciplinary team of theoretical physicists, chemists and biologists who wanted to develop cross-disciplinary techniques that will accelerate work in all three fields. The team was called the Interdisciplinary Theoretical Science Research Group (iTHES).
We soon recognized that dedicated mathematicians could hugely accelerate this project. So, in 2016, iTHES was relaunched as the RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS), and we began recruiting mathematicians. Today, we boast nine mathematicians hailing from both pure and applied fields.
One of the reasons this works is because, while scientists are sometimes hampered by different terminology, theoretical biologists, chemists and physicists already use similar kinds of math. For example, all these areas delve into ‘many-body systems’ (physicists call this statistical mechanics). In physics, these systems could be composed of quarks and gluons, which group together to form protons and neutrons, while in biology they could be cells interacting together to form tissues. Consequently, some modeling techniques can be re-purposed for use across these fields.
Take, for instance, the Markovian lattice model, which I used in condensed-matter physics and elementary particle physics to study quantum questions. It turned out a similar method is used in biology. So, in 2017, we re-purposed the physics model and used it to show how a small deviation in fish-eye patterns leads to the formation of photoreceptor cells in fish retina1. Our finding may have implications for the development of other organism structures, while our method could inform future interdisciplinary collaborations and the use of computer modeling across disciplines. With a bit of extra work, we can probably re-purpose a lot of physics-related modeling software for biologists.
Furthermore, as the detail on DNA comes into focus, both conceptually and under more powerful microscopes, its study is increasingly involving using mathematical fields such as knot theory—DNA is essentially a string of molecules that sometimes becomes entangled like a knot. Examples of how mathematical modeling can benefit the study of DNA have already been demonstrated by Yuji Sakai—but I’ll discuss that below. Theoretical biologists and clinicians also want to make connections between the function of DNA and cells by examining topological, real-space structures using mathematical models. If this is successful, analysis might one day be performed using images and sophisticated mathematics-based modeling alone.
Jumping interdisciplinary barriers
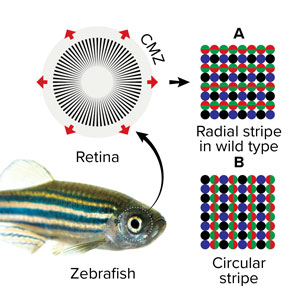 Fish retina pattern mystery explained: The retinas of fish and amphibians grow continuously by adding rings of new cone cells at the periphery, the ciliary marginal zone (CMZ, top left). Zebrafish eyes have four different types of cone cells, which sense blue, ultraviolet and a combination of red and green in two different patterns (right). Biologists already know that these cells are added to the CMZ in a consistent radial pattern, but why they form this pattern and not an equally probable configuration that appears as if the radial pattern was turned 90 degrees (bottom right), wasn't understood. Using a dynamic model from physics known as the Markovian lattice model, a group of researchers in iTHES and iTHEMS, including Tetsuo Hatsuda, were able to help a RIKEN team show that small flaws led to the consistent radial pattern in zebrafish retina. © PaulBull/Getty IMages; © 2018 RIKEN
Fish retina pattern mystery explained: The retinas of fish and amphibians grow continuously by adding rings of new cone cells at the periphery, the ciliary marginal zone (CMZ, top left). Zebrafish eyes have four different types of cone cells, which sense blue, ultraviolet and a combination of red and green in two different patterns (right). Biologists already know that these cells are added to the CMZ in a consistent radial pattern, but why they form this pattern and not an equally probable configuration that appears as if the radial pattern was turned 90 degrees (bottom right), wasn't understood. Using a dynamic model from physics known as the Markovian lattice model, a group of researchers in iTHES and iTHEMS, including Tetsuo Hatsuda, were able to help a RIKEN team show that small flaws led to the consistent radial pattern in zebrafish retina. © PaulBull/Getty IMages; © 2018 RIKEN
Nature reporter Heidi Ledford has noted that interdisciplinary collaboration faces some long-discussed social, publication and funding hurdles. For example, it’s hard for researchers to know which area their work will be appreciated in—which journals to submit to; what departments to apply for jobs with; and, how to get grants. Because of this, some young scientists still feel the need to specialize in traditional subjects to get ahead. However, interdisciplinary complexity hasn’t stopped some incredible successes at iTHES and iTHEMS—particularly when math has been re-purposed across disciplines.
As mentioned above, one example is Yuji Sakai. He has used physics to explore chromosome formation and separation—a fundamental process that nonetheless remained a mystery to biologists for more than 100 years. Sakai was a post-doctoral researcher in nuclear physics. After coming to iTHES, he became fascinated with modeling how long DNA molecule chain copies tangle and then somehow separate during cell division, which occurs in tissue growth and regeneration. For example, in the mitotic phase of cell division, DNA that has been duplicated becomes quite tangled and condenses into characteristic rod-shaped chromosomes. Somehow these chromosomes separate into four chromatids and then rejoin in a different configuration to form two sets of identical chromosomes, which eventually become separate cells.
Sakai used his knowledge of simulations and physics to model this with researchers from RIKEN’s Theoretical Biology Laboratory and Chromosome Dynamics Laboratory, and they found that a cut-and-paste mechanism likely untangles DNA during the separation process2. Since DNA chains contain the macromolecule chromatin, Sakai later showed that DNA interactions can be studied using the same concepts as the macromolecules of polymer physics3. Despite being trained as a nuclear physicist, Sakai is now an assistant professor working on modeling at the University of Tokyo’s Graduate School of Medicine.
The second barrier I mentioned, journals, will pose a decreasing problem. Perhaps because of their heavily mathematical basis, many physics journals are already quite flexible in their subject matter. Sakai’s study, for instance, was published in a specialized interdisciplinary journal, Physical Review E, which is published by the American Physical Society, the world’s second largest organization of physicists. Established in 1993, the journal specifically covers interdisciplinary work in statistical, nonlinear, biological, and soft-matter physics, among other areas. New interdisciplinary journals are cropping up all the time.
Finally, securing funding to support a culture of interdisciplinary work is still perhaps the biggest hurdle, although there are many reasons to be hopeful. Crossovers don’t mean specialties will end. One of the biggest barriers to interdisciplinary work at iTHEMS is the huge amount of specific terminology that has arisen from the organic growth of biology as a field. No physicist can know everything about biology, or vice versa. I also strongly believe specialization is the key to meaningful outcomes. For this reason, iTHEMS is grouped into ‘CELLs’, a name derived from biology. The idea is that they can contain specialists, but that these groups can also evolve to become fused or separated like cells in the body. Several programs at iTHEMS are designed to support interaction between fields, researchers and these CELLs, so that this change and growth can happen naturally (see box).
Ledford notes that big problems often require interdisciplinary responses, while the authors of the The Era of Mathematics report also point out that disseminating mathematical solutions is still “largely about people and relationships, and that personal motivation for engagement in [knowledge exchange]”. Thus, carefully thought-out academic programs like iTHEMS are key to supporting important interdisciplinary work. However, we’re entering a phase in Japan and all over the world where science funding is very outcome oriented. A lot of what iTHEMS is doing is about building structures to support outcomes—we’re building the capacity for young researchers to hop from one field to another. It will probably be five to seven years before we can harvest large-scale results. We see some hope in the fact that the world outside academia is beginning to acknowledge the need for complex computational mathematics, which is set to play a big role in industrial, biological, economic and environmental modeling. Banks, for example, often have access to big data without, perhaps, the knowledge of how to model it in very complex ways. Because of this, one possible avenue of support is to pursue some private funding for our core interdisciplinary facilitation work through industry collaborations. We welcome enquiries.
iTHEMS's unique structure and finding forums to talk across disciplines

Founded in November 2016, iTHEMS is made up of scientists who work in theoretical physics and astrophysics, theoretical biology, pure and applied mathematics, information science and computational science. iTHEMS has ‘Research CELLs’, groups designed to go beyond the boundaries of disciplines. Like biological cells, these groups interact and stimulate each other, and sometimes they may ‘fuse’ or ‘divide’. There are currently four CELLS: Extreme Universe; Life and Evolution; Mathematics and AI; and Future Geometry.
Coffee meetings are also held every Friday, where researchers present their problems to a mixed crowd, and interdisciplinary workshops and lectures are frequent. Successes are hard to predict, but satisfyingly interesting. For example, after hearing a talk by a Google representative, one string theory researcher, Masato Taki, has become a popular author on machine learning and has already developed a well-received code for breast cancer screening.
References
- 1. Ogawa, N., Hatsuda, T., Mochizuki, A., and Tachikawa, M. Dynamical pattern selection of growing cellular mosaic in fish retina. Phys. Rev. E 96, 032416 (2017). doi: 10.1103/PhysRevE.96.032416
- 2. Sakai Y., Tachikawa M. and Mochizuki A. Controlling segregation speed of entangled polymers by the shapes: A simple model for eukaryotic chromosome segregation. Phys. Rev. E 94, 042403 (2016). doi: 10.1103/PhysRevE.94.042403
- 3. Sakai, Y., Mochizuki, A., Kinoshita, K., Hirano, T., Tachikawa, M. Modeling the functions of condensin in chromosome shaping and segregation. PLOS Computational Biology 14(6), e1006152 (2018). doi: 10.1371/journal.pcbi.1006152
- 4. RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS) website
About the Researcher
Tetsuo Hatsuda, Program director, RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS)

Theoretical physicist Tetsuo Hatsuda has spent more than 30 years working in particle and nuclear physics both in Japan and abroad. After 10 years at the University of Tokyo he joined the RIKEN Nishina Center for Accelerator-Based Science as a chief scientist in 2012. In 2013, he launched the Interdisciplinary Theoretical Science Research Group (iTHES), which became the Interdisciplinary Theoretical and Mathematical Sciences Program (iTHEMS) in 2016.
