要旨
理化学研究所(理研)脳科学総合研究センター脳数理研究チームの大泉匡史基礎科学特別研究員、甘利俊一チームリーダー、モナシュ大学の土谷尚嗣准教授らの国際共同研究チームは、ネットワーク内の「情報の統合」を定量化するための数理的な枠組みを提案しました。
私たちの脳が「意識」を生み出すためには、神経細胞同士が密に情報をやりとりすること、つまり情報の統合が必要であると考えられています。例えば、単純なデジタルカメラと脳の情報処理の違いを考えたとき、デジタルカメラの中の多くのフォトダイオードでは、独立に情報処理を行っているだけで情報のやりとりはなく、情報は統合されていません。すなわち、デジタルカメラ自体は見ているものを意識することはできないと考えられます。一方、脳の中ではそれぞれの神経細胞が処理した情報を、神経細胞同士がシナプス[1]を介してやりとりすることによって情報が統合されるため、私たちは豊かな意識体験を持つことができると考えられます。
このことから、「統合情報量(情報の統合の度合い)」を、脳活動をもとに定量化することによって、植物状態や麻酔下の患者など意識状態の判別が困難な状況でも、客観的に意識レベル[2]を測ることができる可能性があります。しかし、これまでに提案された統合情報量の指標には数学的な問題点がありました。
今回、国際共同研究チームは、情報の統合の定量化という目的に向けて「情報幾何学[3]」という手法を用いて、ネットワーク内の統合情報量の新しい指標を見出しました。ネットワークの要素間(脳であれば神経細胞)の因果関係を階層的に定量化する数理的な枠組みを提案し、この枠組みの中で統合情報量を一意的に導き出しました。さらに、同じ枠組みからネットワークの因果性の解析で使われる移動エントロピー[4]などの既存の指標も導出できることを示しました。これによって、従来の数学的問題を解消し、統合情報量、相互情報量、移動エントロピーなどのさまざまな指標の統一的な理解が可能になりました。
本手法は、神経ネットワークの解析に用いることにより意識レベルの定量化につながる可能性があるほか、素子間の因果性を解析する新たな方法論として、ソーシャルネットワークなどのより一般的なネットワークの解析にも適用することができます。今後、複雑なネットワークの新たな解析手法として幅広く利用されると期待できます。
本研究成果は、米国の科学雑誌『Proceedings of the National Academy of Sciences of the United States of America』オンライン版(12月6日付け:日本時間12月7日)に掲載されます。
本研究は、科学技術振興機構(JST) 戦略的創造推進事業 チーム型研究(CREST)「人間と調和した創造的協働を実現する知的情報処理システムの構築」(研究総括:萩田 紀博 株式会社国際電気通信基礎技術研究所 取締役/知能ロボティクス研究所 所長)の研究課題「神経科学の公理的計算論と工学の構成論の融合による人工意識の構築とその実生活空間への実装」(研究代表者:金井 良太 株式会社アラヤ・ブレイン・イメージング 代表取締役)(研究期間:平成27~33年度)の一環で実施されました。
背景
私たちの脳が「意識」を生み出すためには、神経細胞同士が密に情報をやりとりすること、つまり「情報の統合」が必要であると考えられています。例えば、単純なデジタルカメラと脳の情報処理の違いを考えたとき、デジタルカメラでは、内部の多くのフォトダイオードは独立に情報処理を行っているため情報のやりとりはなく、内部で情報は統合されていません。すなわち、デジタルカメラ自体は見ているものを意識することはできないと考えられます。一方、脳の中ではそれぞれの神経細胞が処理した情報を、神経細胞同士がシナプスを介してやりとりすることによって情報が統合されているため、私たちは豊かな意識体験を持つことができると考えられます。
意識の統合情報理論[5]には、脳の中で統合される情報の量、「統合情報量」が意識レベルに対応しているという仮説があります。この仮説が正しければ、植物状態や麻酔下の患者など意識状態の判別が困難な状況でも、脳活動から統合情報量を計測することによって客観的に意識レベルを測ることができる可能性があります。
しかし、これまでに提案された統合情報量の「指標」には数学的な問題点がありました。国際共同研究チームはこの問題点を解消するために、「情報幾何学」を用いて統合情報量の新しい指標の導出を試みました。
研究手法と成果
国際共同研究チームは、ネットワークの要素間の因果的な影響を定量化するための統一的な枠組みを図1のように考えました。因果的な影響とは、過去の状態が未来の状態に与える影響のことです。簡略化するためここでは、ネットワークの要素を二つにして、過去の状態をX=(x1, x2)、未来の状態をY=(y1, y2)と表記します。ただし、要素数が2よりも大きい場合も同様の議論が可能です。“元のネットワーク”のダイナミクスは、過去と未来の状態を合わせた確率分布[6] p(X,Y)(以下、p)で表されます(図1左)。因果的な影響、例えば要素1の過去(x1)から要素2の未来(y2)への影響は、図中のx1とy2を結ぶ斜めの線で表されます。
さらに因果的な影響の大きさを測るために、元のネットワークとは別に“因果的な影響が切断されたネットワーク”を考え、このネットワークの確率分布をq(X,Y)(以下、q)で表します(図1右)。因果的なネットワークの影響が切断されるとは、確率分布qに制約がかかることを意味します。具体的には、例えばx1からy2への因果的な影響が切断されるということは、確率分布qに対してq(y2|x1, x2)=q(y2|x2)という制約が課されることを意味します。この制約は、y2の状態がx1によらず、x2によってのみ決まることを意味しています。
統合情報量で測りたいのは、x1からy2への因果的な影響の大きさとx2からy1への因果的な影響の大きさの二つです。
この理論的な枠組みにおいて因果的な影響の大きさは、元のネットワークの確率分布pと因果的な影響が切断されたネットワークの確率分布qの集合が作る部分空間(部分多様体)Mとの距離を最小にすることによって求められます。これを、情報幾何学を用いて説明したのが図2です。図は確率分布の集合が作る空間を、その中の任意の点はある確率分布を表しています。元のネットワークの確率分布pはこの空間の中の1点です。制約を課されて切断されたネットワークの確率分布の集合qは、この空間の中でMを形成します。pからMに直交するように垂線を下ろすと、pからMに最も近い点q*を見つけることができます。
これはユークリッド幾何学(平らな紙の上に描いた点・直線・平面などを取り扱う図形の学問)において、点と平面の最短距離を求める場合と同じです。因果的な影響の大きさは、pとpに最も近い点q*との“距離”で定量化することができます。確率分布同士の距離を測るには、通常のユークリッド幾何学における距離ではなく、カルバック・ライプラー距離(KL距離)[7]という量を用います。Mが曲がっていない平面である場合、p、q*、Mの中の任意の点qの3点は直角三角形を作ります。このとき、ユークリッド幾何学におけるピタゴラスの定理「x2+y2=z2」と同様の一般化されたピタゴラスの定理「D(p||q*)+D(q*||q)=D(p||q)」が成立し、pに最も近い点q*を容易に求めることができます。
国際共同研究チームはこの枠組みに基づいて、「統合情報量は元のネットワークの確率分布pと、x1からy2およびx2からy1への影響がないという制約を満たす確率分布qとのKL距離の最小値である」と定義しました。数式では次のように表されます。
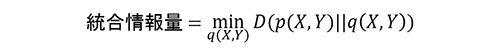
この統合情報量は、「要素1と2の間の相互の因果的な影響の大きさを定量化したもの」として解釈でき、いい換えると「要素1と2の間でどれだけの情報がやりとりされているかを定量化したもの」になります。
また、この枠組みは統合情報量だけでなく、これまでに提案されたさまざまな指標も統一的に導出することができます。ネットワーク全体の過去Xから未来Yへの影響が全て切断されたネットワークの確率分布qを考えると、pとqとのKL距離は、XとYの間の「相互情報量」と呼ばれる量になります(図3(a))。これはネットワーク全体の因果的な影響の“上限”を決める値です。また、元のネットワークの確率分布pと、x1からy2だけの影響を切断したネットワークの確率分布qとのKL距離は、「移動エントロピー」と呼ばれる量になります(図3(b))。
このように同じ数理的枠組みから、統合情報量、相互情報量、移動エントロピーというさまざまな量を統一的に導出することができ、統合情報量の数学的な意味付けが明確化されました。また、これらの量の間には大小関係が成立し、
ネットワーク全体の相互情報量 > 統合情報量 > 移動エントロピー
の関係性が成立することが示されました。この大小関係は図1と図3(a)(b)を比較して、図1の元のネットワークの図から、XからYを結ぶ線がどれだけなくなっているかを見れば明らかです。線を切れば切るほど、pとqの差は大きくなります。
一方、過去に提案された統合情報量の指標もこの枠組みから導出することができます。従来の指標は、x1からy2およびx2からy1への因果的な影響だけでなく、y1とy2の間の同時刻の影響も切断した確率分布qと元のネットワークの確率分布pとのKL距離であることが分かりました(図3(c))。従来の指標を用いると、XとYの間に因果的な影響が全くない、すなわちネットワーク全体に情報がないとき(相互情報量が0のとき)でも、統合情報量は0にならないという問題がありました。しかし新しい指標を用いると、統合情報量はネットワーク全体の相互情報量よりも必ず小さくなるため、この問題を解消できることになります。
今後の期待
今後は、提案した統合情報量の指標を脳活動のデータから計算することで、意識レベルの客観的な定量化ができると考えられます。また本手法は、ネットワークの素子間の因果性を解析するための新たな方法論を提供することになり、神経ネットワークの解析だけでなく、ソーシャルネットワークなどのより一般的なネットワークの解析にも利用できるため、今後、幅広い利活用が期待できます。
原論文情報
- Masafumi Oizumi, Naotsugu Tsuchiya, Shun-ichi Amari, "Unified framework for information integration based on information geometry", Proceedings of the National Academy of Sciences of the United States of America, doi: 10.1073/pnas.1603583113
発表者
理化学研究所
脳科学総合研究センター 脳数理研究チーム
基礎科学特別研究員 大泉 匡史 (おおいずみ まさふみ)
チームリーダー 甘利 俊一 (あまり しゅんいち)
モナシュ大学
准教授 土谷 尚嗣 (つちや なおつぐ)
報道担当
理化学研究所 広報室 報道担当Tel: 048-467-9272 / Fax: 048-462-4715
補足説明
- 1.シナプス
神経細胞同士の情報伝達に関わる構造。情報を伝える細胞と伝えられる細胞の間には約20ナノメートル(nm、1nmは10億分の1m)のすき間がある。情報を伝える細胞はこのすき間に神経伝達物質を放出し、伝えられる細胞側の神経伝達物質受容体がそれを受け取ることにより神経情報が伝わる。 - 2.意識レベル
完全な覚醒から眠い状態、睡眠まで連続的に変化する意識の量。睡眠の中でも、夢を見ているときの睡眠は覚醒時の意識レベルに近く、夢を見ていないときの睡眠は意識レベルが低くなっている状態であると考えられる。他には全身麻酔、てんかん、植物状態などは意識レベルが非常に低い状態、いわゆる無意識の状態である。 - 3.情報幾何学
確率分布の集合からなる空間を考えて、その空間の中に成り立つ幾何学を考える数学の分野。統計学、機械学習、情報理論など確率分布が主要な役割を果たす分野において用いられ、幾何学的な直観的な理解と新しい方法論を提供している。 - 4.移動エントロピー
二つの時系列A、Bが与えられたときにAからBへ因果的な影響を測る方法。Bの未来の値の不確かさ(エントロピー)がAの過去を知ったときにどれだけ減少するかを測るのが移動エントロピー。具体的には、A自身の過去だけを知ったときのAの未来の状態のエントロピーから、AとB両方の過去を知ったときのAの未来の状態のエントロピーを引くことによって、Bの過去がAの過去以上にBの未来に与える影響を定量化する。 - 5.統合情報理論
ネットワークの内部で統合された情報という観点から、意識という現象を数学的に理解しようとする理論。統合情報理論は、意識の現象論から、意識の本質的な性質は「情報」と「統合」であると考え(公理)、ある物理系が意識を生成するためにはネットワーク内部で情報が統合されてなければならないとしている(要請)。ネットワーク内部で統合された情報の量を「統合情報量」という数学的な指標で定義し、統合情報量の大きさが意識の量に対応するという仮説を提唱している。 - 6.確率分布
試行ごとにある確率をもって定まる量(例えば、2個のさいころを振る試行で出た目)を確率変数( X, Y)という。その確率変数の取る値の確率の分布を確率分布 p(X,Y)という。 - 7.カルバック・ライプラー距離(KL距離)
二つの確率分布がどれだけ異なるかを測る情報理論的な量。「距離」と書いているが実際は距離の公理は満たさないため、距離のようなものという方が正しい。確率分布 pと qとのカルバック・ライプラー距離とは、 pを qという分布で近似したときの、情報の損失とも解釈できる。KLはKullback-Leiblerの略。
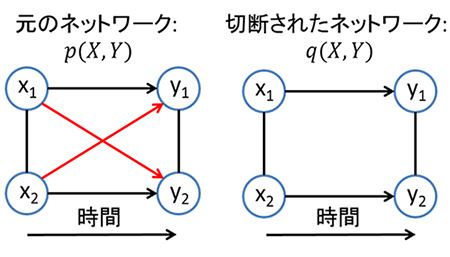
図1 ネットワークの要素間の因果的な影響を定量化するための統一的な枠組み
左: 元のネットワークのダイナミクスは、過去と未来の状態を合わせた確率分布p(X,Y)で表される。因果的な影響、例えば要素1の過去(x1)から要素2の未来(y2)への影響は、図中のx1とy2を結ぶ斜めの線で表される。
右: 因果的な影響が切断されたネットワークでは、確率分布はq(X,Y)で表される。因果的なネットワークの影響が切断されるとは、確率分布qに制約がかかることを意味する。この場合は左側の元のネットワークの2本の赤線の影響が制約を受けている。統合情報量で測りたいのは、x1からy2へ、およびx2からy1への因果的な影響の大きさと因果的な影響の大きさの二つである(赤い矢印)。
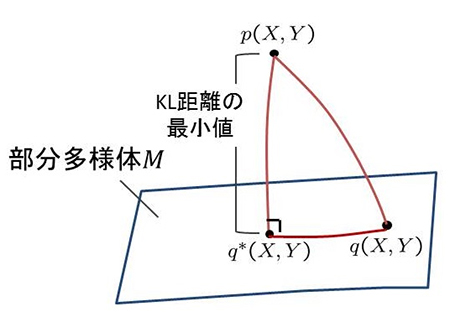
図2 因果的な影響の大きさの求め方
元のネットワークの確率分布p(X,Y)と因果的な影響が切断されたネットワークの確率分布q(X,Y)との距離(KL距離)を、最小化するための幾何学的解釈を表した図。P(X,Y)から、q(X,Y)の集合が作る部分多様体M(青線で囲まれた平面)に直交するように垂線を下ろすと、 p(X,Y)からMに最も近い点q*(X,Y)が求められる。このP(X,Y)とq*(X,Y)の距離がKL距離の最小値である。
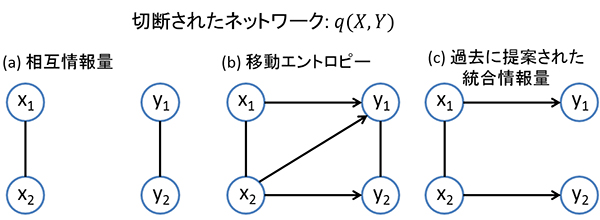
図3 切断されたネットワーク
(a) 相互情報量とは、元のネットワークの確率分布pとネットワーク全体の過去Xから未来Yへの影響が全て切断されたネットワークの確率分布qとのKL距離である。相互情報量はネットワーク全体の因果的な影響の上限を決める値である。
(b) 移動エントロピーとは、元のネットワークの確率分布pとx1からy2だけの影響が切断されたネットワークの確率分布qとのKL距離である。
(c) これまでに提案された統合情報量の指標も、元のネットワークの確率分布pと切断されたネットワークの確率分布qとのKL距離の最小値として統一的に導出することが可能である。y1とy2の間の同時刻の影響も遮断していることが今回提案した新しい統合情報量の指標(図1)との違い。
