Mar. 28, 2022 Press Release Computing / Math
Chaos theory provides hints for controlling the weather
Under a project led by the RIKEN Center for Computational Science, researchers have used computer simulations to show that weather phenomena such as sudden downpours could potentially be modified by making small adjustments to certain variables in the weather system. They did this by taking advantage of a system known as a “butterfly attractor” in chaos theory, where a system can have one of two states—like the wings of a butterfly—and that it switches back and forth between the two states depending on small changes in certain conditions.
While weather predictions have reached levels of high accuracy thanks to methods such as supercomputer-based simulations and data assimilation, where observational data is incorporated into simulations, scientists have long hoped to be able to control the weather. Research in this area has intensified due to climate change, which has led to more extreme weather events such as torrential rain and storms.
There are methods at present for weather modification, but they have had limited success. Seeding the atmosphere to induce rain has been demonstrated, but it is only possible when the atmosphere is already in a state where it might rain. Geoengineering projects have been envisioned, but have not been carried out due to concerns about what unpredicted long-term effects they might have.
As a promising approach, researchers from the RIKEN team have looked to chaos theory to create realistic possibilities for mitigating weather events such as torrential rain. Specifically, they have focused on a phenomenon known as a butterfly attractor, proposed by mathematician and meteorologist Edward Lorentz, one of the founders of modern chaos theory. Essentially, this refers to a system that can adopt one of two orbits that look like the wings of a butterfly, but can change the orbits randomly based on small fluctuations in the system.
To perform the work, the RIKEN team ran one weather simulation, to serve as the control of “nature” itself, and then ran other simulations, using small variations in a number of variables describing the convection—how heat moves through the system—and discovered that small changes in several of the variables together could lead to the system being in a certain state once a certain amount of time elapsed.
According to Takemasa Miyoshi of the RIKEN Center for Computational Science, who led the team, “This opens the path to research into the controllability of weather and could lead to weather control technology. If realized, this research could help us prevent and mitigate extreme windstorms, such as torrential rains and typhoons, whose risks are increasing with climate change.”
“We have built a new theory and methodology for studying the controllability of weather,” he continues. “Based on the observing system simulation experiments used in previous predictability studies, we were able to design an experiment to investigate predictability based on the assumption that the true values (nature) cannot be changed, but rather that we can change the idea of what can be changed (the object to be controlled).”
Looking to the future, he says, “In this case we used an ideal low-dimensional model to develop a new theory, and in the future we plan to use actual weather models to study the possible controllability of weather.”
The work, published in Nonlinear Processes of Geophysics, was done as part of the Moonshot R&D Millennia program, contributing to the new Moonshot goal #8.
Rate this article
Reference
Contact
Takemasa Miyoshi, Team Leader
Data Assimilation Research Team
RIKEN Center for Computational Science
Jens Wilkinson
RIKEN International Affairs Division
Tel: +81-(0)48-462-1225
Email: gro-pr [at] riken.jp
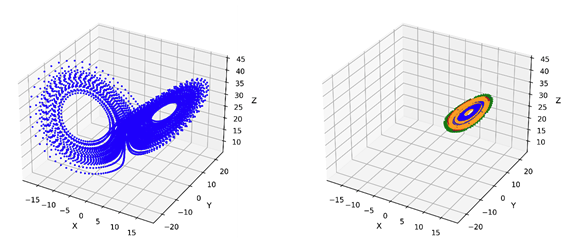
The phase space of the three-variable Lorenz model
The left panel shows the Lorenz’s butterfly attractor from the natural run (the initial run used as nature) without control, and the right shows the natural run compared to various controls.
