May 22, 2020 Research Highlight Physics / Astronomy
Superconductivity emerges in semiconductor on doping with valence-skipping metal
A long-known semiconductor that turns into a superconductor on doping provides a good system for exploring the effects of valence skipping
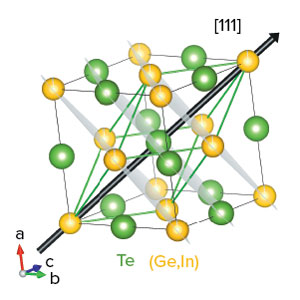 The crystal structure of the semiconductor germanium telluride. The green spheres are tellurium atoms and the gold ones are germanium or indium atoms. The system becomes superconducting when sufficient germanium ions have been replaced with indium. Reprinted, with permission, from Ref. 1. Copyright (2020) by the American Physical Society.
The crystal structure of the semiconductor germanium telluride. The green spheres are tellurium atoms and the gold ones are germanium or indium atoms. The system becomes superconducting when sufficient germanium ions have been replaced with indium. Reprinted, with permission, from Ref. 1. Copyright (2020) by the American Physical Society.
An ordinary semiconductor that superconducts at very low temperatures can lose its superconductivity and then develop a new superconducting phase on increasing the amount of the metal indium added to it, RIKEN physicists have discovered1. This system may provide clues about how to produce materials that superconduct at higher temperatures by exploiting the ‘valence-skipping’ property of indium—one of more than ten elements possessing this ability.
Superconductors conduct electricity without resistance. They can be broadly categorized into conventional ones whose superconducting mechanism is known and unconventional ones whose mechanism still remains to be discovered. Although scientists know how conventional superconductors work, they want to probe them more to discover ways to increase the temperature at which they superconduct.
Some materials are inherently superconducting, while others can be made to superconduct by altering some property such as applying pressure or tinkering with their chemical composition. One such way is to swap out some atoms of one of the elements in a material with those of another one.
Now, Markus Kriener of the RIKEN Center for Emergent Matter Science and co-workers have found that the semiconductor germanium telluride (GeTe; Fig. 1) can be made into a conventional superconductor by replacing some of its germanium atoms with indium ones.
 Markus Kriener and his co-workers have investigated the emergence of superconductivity in the semiconductor germanium telluride by doping with valence-skipping indium.© 2020 RIKEN
Markus Kriener and his co-workers have investigated the emergence of superconductivity in the semiconductor germanium telluride by doping with valence-skipping indium.© 2020 RIKEN
This system is particularly interesting because indium seems to switch its valence state from three to one when the doping level increases, skipping the intermediate state of two. In pure germanium telluride, the metal germanium gives two electrons to tellurium, and thus both elements have a valence of two. But when indium replaces a germanium ion, it strongly prefers to donate one electron (a valence state of one) or three electrons (a valence state of three) to avoid ending up with a single electron in its outer shell. The team thinks this valence skipping in indium plays a key role in the emergence of a new superconducting phase in germanium telluride.
In addition, the researchers found that many of the properties of the system had their largest or smallest values when 12% of the germanium had been replaced by indium. They also ascribed this to the valence state of indium switching from three to one. “It was quite surprising that so many features of this system change at a single doping concentration,” says Kriener. “We realized that this is a pivotal point of all our observations.”
These findings should help scientists to use valence skipping to produce superconductivity in other systems. “Our work contributes to the understanding of the driving forces and mechanisms of superconductivity, not only from the viewpoint of fundamental research in superconductivity but also of materials-design research,” says Kriener.
Related contents
- Modified nickelate materials could serve as useful test-beds for understanding high-temperature
- Frustration explains differences in superconductivity in molecular conductors and cuprates
- Light pulses provide a new route to enhance superconductivity
References
- 1. Kriener, M., Sakano, M., Kamitani, M., Bahramy, M. S., Yukawa, R., Horiba, K., Kumigashira, H., Ishizaka, K., Tokura, Y. & Taguchi, Y. Evolution of electronic states and emergence of superconductivity in the polar semiconductor GeTe by doping valence-skipping indium. Physical Review Letter 124, 047002 (2020). doi: 10.1103/PhysRevLett.124.047002
