2016年3月19日
理化学研究所
ディラック電子系に潜む普遍性を実証
-世界最大規模のシミュレーションで金属-絶縁体転移の臨界指数を決定-
要旨
理化学研究所(理研)計算科学研究機構 量子系物質科学研究チームの柚木清司チームリーダー、大塚雄一研究員、サンドロ・ソレラ客員主管研究員の研究チームは、グラフェン[1]などで見られる質量ゼロの2次元ディラック電子[2]系において、電子間の相互作用が引き起こす金属から絶縁体への相転移(金属-絶縁体転移)が、普遍的な性質を持つことを世界最大規模のシミュレーションにより明らかにしました。
電子間の相互作用による金属-絶縁体転移は、物性物理学の最も基本的な現象です。その研究は60年以上の歴史があるにも関わらず、どのように相転移するかその具体的な様相が明らかになった例はこれまで限られていました。
この研究には大規模なシミュレーションが不可欠です。研究チームは、独自に開発した量子モンテカルロ法[3]によるシミュレーションをスーパーコンピュータ「京」[4]で実行しました。研究対象として、蜂の巣状をしたハニカム格子とπフラックスを持つ正方格子[5]上における2次元ハバード模型[6]を用いました。これら二つの模型は格子の形状が大きく異なるにもかかわらず、質量ゼロのディラック電子系を構成しています。金属-絶縁体転移の「臨界指数[7]」を正確に評価するために、各クラスタの格子点の数をNとして、N=2,592の系までシミュレーションを実行しました。これは、先行研究の計算量の約100倍に相当し、現在までの世界最大規模のシミュレーションを実現したことになります。
研究チームは、金属-絶縁体転移に伴う反強磁性相の強さの指標となる秩序変数に対して有限サイズスクリーン解析[8]を両模型で独立に行いました。その結果、臨界指数は統計誤差の範囲内で一致することが分かりました。次に、より直接的に金属-絶縁体転移の指標となる準粒子重み[9]に対する計算を行いました。その結果、この物理量から得られる別の臨界指数も両模型で一致することが確認されました。以上により、普遍性クラス[10]が存在することを示しました。
今回の成果は、銅酸化物高温超伝導体やスピン液体[11]などを示す分子性導体といった、ディラック電子を構成しない電子間相互作用が強い系でみられる金属-絶縁体転移を解明する第一歩となると期待できます。また、ディラック電子系における金属-絶縁体転移の基礎理論は、高エネルギー物理学分野で古くから議論されていたGross-Neveu模型[12]と密接に関連しており、物性物理から素粒子物理までスケールを超えた臨界現象[7]の理解が可能になりました。
本研究は、米国の科学雑誌『Physical Review X』)に掲載されるのに先立ち、オンライン版(3月18日付け:日本時間3月19日)に掲載予定です。
背景
物質中の電子はその置かれた環境により、元の電子とは性質が大きく異なる粒子として振る舞うことがあります。その顕著な例が、グラフェンの中に現れる「ディラック電子」です。ディラック電子は量子力学に相対論的効果を取り込んだ運動方程式(ディラック方程式[2])に従う電子で、通常は電子の速度が光速に近い状況で問題とされるものです。しかしグラフェン(炭素原子が2次元上に並んだ層状物質)中に存在する電子は、速度がそれほど速くないにも関わらず、骨格となる炭素原子ネットワークの蜂の巣(ハニカム)構造に起因して、質量がゼロのディラック粒子として振る舞うことが知られています。
グラフェンの中に現れるディラック電子は質量がゼロとなっていますが、もともとの電子が持っていた電荷およびスピン(電子の自転)の自由度は失われていません。したがって、物質中で多数のディラック電子が集まって示すマクロな電気的・磁気的な性質が、孤立した電子とどう違うかという点が、物性科学的には興味を持たれています。その中で最初に注目されるポイントは、それが「金属であるか絶縁体であるか」という点です。ディラック電子の集団は電子が全く自由に動き回る場合は「半金属」となりますが、電荷間に働く電気的斥力(クーロン力)が強くなると、質量がゼロであったディラック電子が質量を持つようになり、絶縁体に相転移します。またそれに伴い、絶縁体相になると局在した電子の間でスピンが隣同士で逆方向を向いて整列し、全体として磁気モーメント(磁力の大きさと向きを表すベクトル量)を持たない「反強磁性状態」となります。このような電子間相互作用によって質量ゼロのディラック電子としての性質が失われていく現象は、物性分野ではこれまで主としてグラフェン研究の関連において基礎論的な側面から研究されてきました。
一方、最近の進展として、この現象を記述する有効的な理論が素粒子分野で古くから議論されてきたGross-Neveu模型と同等であるとの指摘がなされ注目を集めています。これにより、グラフェンで期待される金属から絶縁体への相転移(金属-絶縁体転移)の問題と、素粒子理論におけるカイラル対称性の破れ[13]という問題が、対象もエネルギースケールも全く異なるにも関わらず、同じ普遍性を持つとの認識が生まれ、分野を横断した学際的な研究が展開されています。
電子間相互作用により誘起される金属-絶縁体転移の性質の解明は、物性物理学における最も基本的な問題であり、その研究はこれまで60年以上の長い歴史があります。この問題は本質的に量子多体問題[14]であり、今までの研究では、解析的な手法でも数値シミュレーションでも、なにがしかの近似に頼らざるを得ないものでした。そのためディラック電子系を舞台とする金属-絶縁体転移の普遍性を明らかにすることは、金属-絶縁体転移のメカニズムを明らかにする最初の一歩になるものと期待されています。
そこで研究チームは、2次元格子上で定義された質量ゼロのディラック電子系が実現する2つの異なる模型で起こる金属-絶縁体転移の臨界指数を、スーパーコンピュータ「京」を用いた世界最大規模のシミュレーションを実行することにより世界最高精度で明らかにすることを目標としました。
研究手法と成果
研究チームは、ハニカム格子およびπフラックスを持つ正方格子(図1)上における2次元ハバード模型を研究対象として選びました。これらは、格子形状が異なるにも関わらず質量ゼロのディラック電子系を構成しています(図2)。また、幾何学的フラストレーション[15]を含まないため、量子モンテカルロ法による大規模な数値シミュレーションが可能です。計算にかかる時間は対象とするクラスタに含まれる格子点の数Nの3乗に比例します。金属-絶縁体転移の臨界指数を正確に評価するためには極めて大きなクラスタサイズまで計算する必要があるため、研究チームは「京」を利用しました。用いた計算プログラムは高度に最適化されており、計算機の理論最高性能に対して80%以上の効率で計算できます。これにより、最大でN=2,592の系まで量子モンテカルロ法による計算を行いました。これは、これまで最大の計算量であったドイツの研究グループによる先行研究注)のN=648に比べると、計算量で約100倍に相当し、「京」を用いることで初めてこの規模の計算が可能になりました。
まず、金属-絶縁体転移に伴う反強磁性相の強さの指標となる秩序変数(ms)をサイズの異なるいくつかのクラスタ上で量子モンテカルロ法により計算し、この量に対して「有限サイズスケーリング解析」を行うことで臨界指数を求めました。この解析には京都大学の原田健自博士によって開発された、ベイズ推定に基づくフィッティング・アルゴリズムを利用しました。量子モンテカルロ法はサンプリングに基づく方法のため、計算結果には必然的に統計誤差が含まれます。臨界指数の値から普遍性クラスの存在を実証するには、この誤差の影響を定量的に評価することが不可欠です。そのため、まず統計誤差自体がなるべく小さくなるよう、「京」を活用した大規模並列計算による世界最高精度の計算を実行し、さらにデータ解析の段階ではリサンプリング法による慎重な誤差評価を行いました。図3に示すように、計算結果はこの解析法に非常に良く適合しており、2つの模型に対して独立に計算された臨界指数(β、ν)は統計誤差の範囲内で一致することが分かりました。
また、より直接的に金属-絶縁体転移の指標となる準粒子重みに対する計算も行い、この物理量から得られる別の臨界指数(ηψ)も両模型で一致することが確認できました(図4)。これらの結果から、質量ゼロの2次元ディラック電子系において、電子間相互作用によって誘起される金属-絶縁体転移には普遍性クラスが存在することが実証できました。
さらに、より詳しく金属-絶縁体転移の特徴を調べるため、電子の速度に対応するフェルミ速度(電子を波として捉えた場合の群速度)に関する計算も行いました。その結果、従来の理論では絶縁体化に伴い、電子の準粒子重みがゼロになるとともに必然的にフェルミ速度もゼロに繰り込まれていくことが予測されていましたが、それに反してディラック電子系では準粒子重みは確かにゼロになるのですがフェルミ速度は有限の値のまま保たれることを示す結果が得られました。
注)Z. Y. Meng, T. C. Lang, S. Wessel, F. F. Assaad, and A. Muramatsu, "Quantum Spin Liquid Emerging in Two-Dimensional Correlated Dirac Fermions," Nature 464, 847 (2010).
今後の期待
本研究では、2つの異なる格子模型を例にとり、質量ゼロのディラック電子系で起こる金属-絶縁体転移に普遍性クラスが存在することを、世界最大規模のシミュレーションによって実証しました。Gross-Neveu模型の研究から、ディラックフェルミオン(粒子)系で起こる対称性の破れは少なくとも3つのクラスに別けられることが知られています。本研究で明らかにした普遍性クラスは「カイラル・ハイゼンベルグ」クラスに対応しています。本研究で高精度に決定した臨界指数は、今後、「カイラル・ハイゼンベルグ」転移を特徴づける標準指数になるものと期待できます。残り2つのクラスのうち、「カイラル・イジング」クラスを特徴付ける臨界指数は、最近の数値シミュレーションにより、高精度で得られはじめています。しかし、「カイラル・XY」クラスを特徴付ける臨界指数は、高精度には決定されていません。今後の進展が期待できます。
また本研究により、質量ゼロのディラック電子系で実現する電子間相互作用により誘起される金属から絶縁体への転移が、電子の速度が有限に保たれたまま、電子の準粒子重みが金属側から転移点に向かってゼロになることが本質的であることが分かりました。この振る舞いが、ディラック電子系のみでなく他の系でも普遍的に現れるかどうかを明らかにすることが、電子間相互作用により誘起される金属-絶縁体転移の本質を理解する鍵です。今後のさらなる研究が待たれます。
原論文情報
- Yuichi Otsuka, Seiji Yunoki, and Sandro Sorella, "Universal quantum criticality in the metal-insulator transition of two-dimensional interacting Dirac electrons", Physical Review X, doi: 10.1103/PhysRevX.6.011029
発表者
理化学研究所
計算科学研究機構 研究部門 量子系物質科学研究チーム
チームリーダー 柚木 清司(ゆのき せいじ)
研究員 大塚 雄一(おおつか ゆういち)
客員主管研究員 サンドロ・ソレラ(Sandro Sorella)
報道担当
理化学研究所 広報室 報道担当Tel: 048-467-9272 / Fax: 048-462-4715
補足説明
- 1.グラフェン
炭素原子が2次元上に並んだ層状物質。各炭素原子はsp2結合により正六各形がつながった蜂の巣(ハニカム)状の格子を組む。 - 2.ディラック電子、ディラック方程式
量子力学に相対論的効果を取り込んだ運動方程式(ディラック方程式)に従う電子。 - 3.量子モンテカルロ法
量子力学に従う多数の粒子系の物理量を計算する計算手法。多自由度の積分計算を、重み付きサンプリングで統計的に評価を行う。 - 4.スーパーコンピュータ「京」
文部科学省が推進する「革新的ハイパフォーマンス・コンピューティング・インフラ(HPCI)の構築」プログラムの中核システムとして、理研と富士通が共同で開発を行い、2012年9月に共用を開始した計算速度10ペタFLOPS級のスーパーコンピュータ。 - 5.πフラックスを持つ正方格子
正方格子の各単位格子当たりに量子化磁束の半分がかかっている状態。銅酸化物高温超伝導体を記述する平均場状態の1つ。 - 6.ハバード模型
クーロン相互作用により互いに強く相互作用している電子系を記述する最も基本的な格子模型。電子の運動エネルギー項、および同じ格子点に電子が存在するときのクーロン斥力でハミルトニアン(系全体のエネルギー量)が表される。 - 7.臨界指数、臨界現象
臨界現象とは、物質の状態が突然変化する点(臨界点)において、種々の物理量がその相転移に特有な振る舞いを示すこと。臨界指数は、臨界現象を示す点(臨界点)において物理量が示すべき乗則を特徴づける指数。同じ普遍性クラスに属する臨界現象では、この指数が同じ値を取る。 - 8.有限サイズスケーリング解析
臨界点近傍におけるいくつかの有限サイズのクラスタ上で計算された物理量から臨界指数を求める手法。 - 9.準粒子の重み
相互作用をし合う多数の電子集団の中で、それぞれの電子が「個別粒子」としての性質を示す度合いを表す量。相互作用がない場合は1であり、個別粒子としての性質が完全に失われた場合はゼロとなる。 - 10.普遍性クラス
繰り込み群の考え方に基づいて、臨界現象を分類したもの。さまざまな臨界現象が模型の詳細には依らず、系の次元や秩序変数の対称性といった小数のパラメータにより分類される。 - 11.スピン液体
量子力学的な揺らぎにより、絶対零度(-273.15℃)まで冷やしても、(反)強磁性等のスピンの方向に関する空間的な秩序構造を示さない物質の状態。 - 12.Gross-Neveu模型
1974年にDavid GrossとAndré Neveuによって導入された、量子色力学(QCD)の有効模型。四体相互作用項を持つディラック電子に関する場の理論を記述する。QCDは、原子核を構成するクォークとその間に働く強い相互作用を媒介するグルーオンが従う物理法則であり、素粒子の標準理論の一部である。 - 13.カイラル対称性の破れ
粒子の運動の進行方向に対して、スピンが左巻きか右巻きかを区別する対称性。この対称性が破れることで粒子に質量が生じる。 - 14.量子多体問題
物質中の電子といった、相互作用し合う量子力学的粒子が多数集まった系を取り扱う問題。 - 15.幾何学的フラストレーション
系の微視的な相互作用の間に競合があり、すべての相互作用に関して最適な配置を取りえない状態。
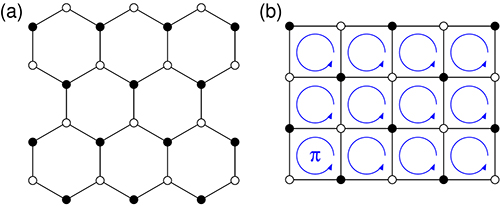
図1 ハニカム格子およびπフラックスを持つ正方格子の格子構造
(a)ハニカム格子。正六各形を隙間なく並べた蜂の巣(ハニカム)のような構造を指す
(b)πフラックスを持つ正方格子。正方格子の各単位格子当たりに量子化磁束の半分がかかっている状態を青線で示している。
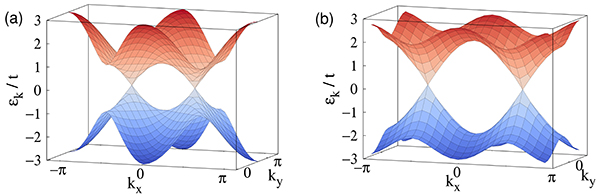
図2 電子間相互作用がない場合の電子のエネルギー分散関係
(a)がハニカム格子上における2次元ハバード模型、(b)がπフラックスを持つ正方格子上における2次元ハバード模型の場合。垂直軸がエネルギー、面内の軸は波数(kxおよびky、単位長あたりの波の数で、波長の逆数)を表す。電子が取りうる電子状態をバンド構造という。両模型とも電子が詰まっている価電子バンド(青色)と空の伝導バンド(赤色)が波数の異なる2点においてエネルギーεk/t=0で接していて、その2点がディラック点に対応している。その周りでのエネルギー分散は波数に対して線形となっており、質量ゼロのディラック電子を構成していることが分かる。
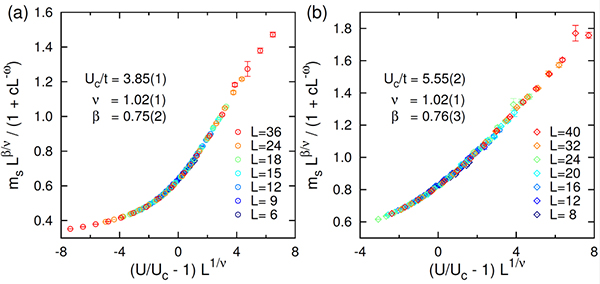
図3 反強磁性秩序変数msに関する有限サイズスケーリング解析の結果
(a)がハニカム格子上における2次元ハバード模型、(b)がπフラックスを持つ正方格子上における2次元ハバード模型の結果。有限サイズクラスタ(一辺の長さL)内で反強磁性秩序変数msを、それぞれ異なる電子間相互作用(ハバード斥力U)の関数として、量子モンテカルロ法により計算した。その結果が1つの滑らかな曲線に乗るように相転移を特徴づける「臨界指数(β,ν)」および「相転移点(臨界点Uc)」を決定した。(a)と(b)で、臨界指数(β,ν)が統計誤差の範囲で一致していることが分かる。tは、最近接サイト間の電子の飛び移りの大きさを表す量。
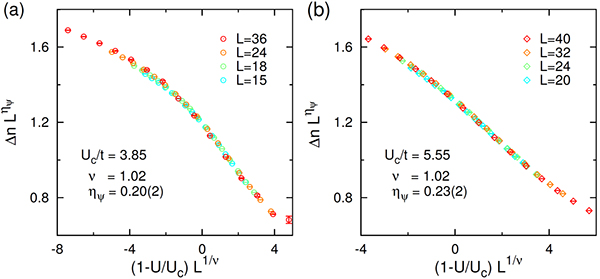
図4 準粒子重みΔnに関する有限サイズスケーリング解析の結果
(a)がハニカム格子上における2次元ハバード模型、(b)がπフラックスを持つ正方格子上における2次元ハバード模型の結果。有限サイズクラスタ(一辺の長さL)内で準粒子重みΔnを、それぞれ異なる電子間相互作用(ハバード斥力U)の関数として、量子モンテカルロ法により計算した。その結果が1つの滑らかな曲線に乗るように「臨界指数ηψ」を決定した。「臨界点Ucおよび指数ν」の値は図3で決定されたものを用いた。(a)と(b)で、臨界指数ηψが統計誤差の範囲で一致していることが分かる。tは最近接サイト間の電子の飛び移りの大きさを表す量。
