要旨
理化学研究所(理研)望月理論生物研究室の森史協力研究員と望月敦史主任研究員(理論科学連携研究推進グループ階層縦断型理論生物学研究チーム チームリーダー、数理創造プログラム副プログラムディレクター)の研究チームは、“ブーリアンネットワークの固定点数の平均値(平均固定点数)が、ある広い条件の下で1になる”という新しい定理を証明しました。
遺伝子[1]のオン・オフ、意見の賛成・反対など、2つの状態で表される要素が相互作用し合う系をモデル化したものを「ブーリアンネットワーク」といいます。このモデルは、ある初期状態から出発すると、それ以上状態が変わらない「固定点」か、状態が周期的に変わり続ける「振動解」のどちらかに落ち着きます。系の持つ固定点の数の問題は、細胞の種類の多様性や意見収束の実現性と密接に関係しているため、その理論研究ではさまざまなアプローチがとられてきました。しかし、固定点数はネットワークのつながり方(トポロジー)とブール関数[2]の割り振り方の両方に依存することから一般にケースバイケースとなり、広い条件下での理論的記述は困難です。そのため、任意のトポロジーを持つブーリアンネットワークでは、ブール関数の割り振り方にさまざまなバイアス(偏り)がある場合の、典型的な固定点数を記述する理論の構築には、これまで誰も成功していませんでした。
今回、研究チームはネットワークを任意のトポロジーに固定し、各要素のブール関数をさまざまな確率分布に従ってランダムに割り振ると仮定した状況で「確率的に中立なリンクの集合がフィードバックアークセット(Feedback Arc Set)であるならば、固定点数の平均値は1である」という、広い条件下で成立する極めて簡潔な定理を導出しました。
ブーリアンネットワークが生命現象の基礎である遺伝子制御系のモデルとして提案されて約半世紀が経過しました。近年では社会現象のモデルとしても注目されています。今回発見した定理は、ブーリアンネットワークを用いた表現が妥当である全ての系に対して適用することができます。また、証明の際に複雑な数式を簡単化する鍵となった新しい不変量による理論的手法は、振動解の数やその周期の長さなど固定点数以外の特徴量の解析にも応用できる可能性があります。
本研究成果は米国の科学雑誌『Physical Review Letters』掲載に先立ちオンライン版(7月12日付け:日本時間7月13日)に掲載される予定です。
本研究は、科学技術振興機構(JST)戦略的創造研究推進事業(CREST)「生命動態の理解と制御のための基盤技術の創出(研究総括:山本雅)」の一環として行われました。
背景
遺伝子のオン・オフ、神経細胞[3]の発火・休止、意見の賛成・反対のように、2つの状態で表される要素が相互作用し合って多彩なダイナミクスを生み出す系は、生物系、社会系を問わず数多くみられます。遺伝子制御[4]、神経回路[5]、意見交換などのネットワークが、その例です。Aの遺伝子がオンになっているときだけBの遺伝子がオンになったり、またCさんとDさんが賛成なら賛成したがる人が、Eさんも賛成となると途端に反対に回ったりと、各要素は周囲の状況に応じて状態を決める“性質”や“性格”を持っています。それをブール関数(Boolean Function)と捉えてモデル化したものを「ブーリアンネットワーク(Boolean network)」といいます。
入力と出力の関係を表す「有向ネットワーク[6]」で互いにつながった各要素の状態(0か1)は、ブール関数に従って更新されます。系全体の状態は、ある初期状態から出発すると、それ以上は状態が変わらない「固定点」か、状態が周期的に変わる「振動解」のどちらかに行き着きます(図1左)。
系に固定点が何個あるかという問題は重要です。意見形成プロセスのモデルと捉えた場合、固定点が存在しないことは、いつまでたっても意見を決められない人が必ず出てくることを意味します。また、細胞の分化[7]では、固定点に対応すると考えられる遺伝子発現パターンが細胞の種類を決定しているので、細胞の種類に多様性が存在するためには、系が多くの固定点を持つ必要があります(図1右)。
しかし、単純な方法でランダムに構築されたブーリアンネットワークでは、要素数を増やしても固定点は平均1個しか存在しないことが指摘されています。従って、固定点を多様に作り出すには、うまくブール関数を選んだり、ネットワークを組んだりするような精巧な機構の存在が予想されます。
ブーリアンネットワークのダイナミクスは一般に、系のネットワークのつながり方(トポロジー)とブール関数の選び方の両方に依存します。そのため、任意のトポロジーを持つブーリアンネットワークの固定点の数を、ブール関数の選び方にさまざまなバイアス(偏り)が存在する条件下で解析するのは、大変に複雑な問題であり、一般公式はありませんでした。
研究手法と成果
研究チームは、ブーリアンネットワークを任意のトポロジーに固定し、各要素のブール関数をさまざまな「確率分布」に従ってランダムに割り振ると仮定した状況で、広い条件下で固定点の数の平均値を記述する定理を導き出しました(図2)。
まず、「あるリンクが確率的に中立である」という概念を導入しました(図3)。直感的には、そのリンクが“活性の役割”と“抑制の役割”を果たす確率が等しいことを意味しています。数学的には、ブール関数を扱う理論で用いられる「Negation同値[8]」という関係性を使って定義しました。Negation同値関係を満たすブール関数を用いて表現された和が、ある種の不変量[9]になっているという事実が、定理の証明の鍵となっています。
また、グラフ理論でよく知られた概念である「フィードバックアークセット(Feedback Arc Set:FAS)」を用いました。FASとは、それを取り除くとネットワークから有向サイクル[6]が消失するリンクの集合で定義されます(図2)。FASは一般に、唯一でなく、また最小サイズである必要もありません。新しく導かれた定理は、“確率的に中立なリンクの集合がFASであるならば、固定点数の平均値(平均固定点数)は1である”というものです。
図4の例を用いて説明すると、左の有向ネットワークで、ピンクの太い矢印で表されたリンクが確率的に中立であれば、他の条件には依らずに平均固定点数が1であるという、非常に強い主張を持つ定理になっています。図4の例は小さいネットワークですが、要素数が数万個といった大きいネットワークに対しても適用可能です。この定理は、ネットワークのトポロジーだけを調整しても、平均固定点数を増やせないことを意味しています。
さらに、別の公式として、サイクル全体で確率中立が破れている場合の平均固定点数は、ポジティブフィードバック[10]が優勢なら1より増え、ネガティブフィードバック[11]が優勢なら1より減ることも示しました。ポジティブフィードバックはこれまで、多様な固定点を生み出すための必要条件としては知られていましたが、本研究で平均固定点数を大きくするための十分性を証明したことになります。
今後の期待
ブーリアンネットワークが、生命現象の基礎である遺伝子制御系のモデルとして提案されたのは、約半世紀も前のことです。複雑な生物の仕組みを少しずつ理解するために、また、モデルがもたらす魅力的な数理の問題を解き明かすために研究は続けられ、近年では社会現象のモデルとしても再注目されています。このような背景の中、本定理は発見されました。
本定理は、ブーリアンネットワークでの記述が妥当である全ての系(任意のトポロジー、任意のサイズ)に対して適用することができます。適用時にはFASが確率中立であるかどうかのチェックだけで済むため、高い実用性を持ちます。本定理を証明する過程で複雑な数式を簡単化する鍵となったのは、新しい不変量の導入でしたが、同じような方法で不変量を適切に導入することにより、固定点のみならず、振動解の数やその周期の長さなど他の特徴の解析が大きく前進する可能性があります。
原論文情報
- Fumito Mori and Atsushi Mochizuki, "Expected Number of Fixed Points in Boolean Networks with Arbitrary Topology", Physical Review Letters
発表者
理化学研究所
主任研究員研究室 望月理論生物学研究室
協力研究員 森 史(もり ふみと)
主任研究員 望月 敦史(もちづき あつし)
(理論科学連携研究推進グループ 階層縦断型理論生物学研究チーム チームリーダー 、数理創造プログラム 副プログラムディレクター)
報道担当
理化学研究所 広報室 報道担当
Tel: 048-467-9272 / Fax: 048-462-4715
お問い合わせフォーム
科学技術振興機構 広報課
Tel: 03-5214-8404 / Fax: 03-5214-8432
jstkoho [at] jst.go.jp(※[at]は@に置き換えてください。)
産業利用に関するお問い合わせ
理化学研究所 産業連携本部 連携推進部お問い合わせフォーム
補足説明
- 1.遺伝子
細胞の核の中にあり、オンの状態では特定のタンパク質が作られ、オフの状態では作られない。 - 2.ブール関数
0か1で表される入力値の集合に対して、0か1の出力を返す関数。例えば、f(0,0)=1, f(0,1)=0, f(1,0)=0, f(1,1)=0を満たす関数fは、2つの入力変数の両方が0のときだけ1を出力する2変数ブール関数。 - 3.神経細胞
神経系を構成する細胞。活動電位が発生しているオンの状態と、発生していないオフの状態を取り得る。 - 4.遺伝子制御
遺伝子Aがタンパク質を作ることで、遺伝子Bがタンパク質を作りやすくなったり、逆に作りにくくなったりするとき、遺伝子AがBを制御するという。遺伝子間の制御関係を矢印で表したものを、遺伝子制御ネットワークと呼ぶ。 - 5.神経回路
神経細胞がシナプス結合によりネットワークを形成したもの。 - 6.有向ネットワーク、有向サイクル
リンクに向きが定義されたネットワークを有向ネットワークと呼ぶ。有向ネットワーク上で、リンクの向きに沿って一周できる経路を有向サイクルと呼ぶ。スタート地点から出てそのままその地点に戻る自己ループや、スタート地点から隣に動いてすぐに逆向きに戻ってくる往復経路も、有向サイクルに含まれる。 - 7.細胞の分化
受精卵が細胞分裂し、いろいろな種類の細胞に分かれていく過程。 - 8.Negation同値
関数 g(x,y,z)が、 g(x,y,z)=f(x,y,z)のように、関数 fのある入力変数の否定( x=0なら x=1、 x=1なら x=0)で定義されるとき、関数 fと gはNegation(否定)同値関係にあるという。 - 9.不変量
変換に対して値を変えない量。本研究では、変数の否定という変換に対して、変わらない量。 - 10.ポジティブフィードバック
ブーリアンネットワークでは、活性の役割のリンクを+1、抑制の役割のリンクを-1で表したとき、サイクルを一周したときの数字の掛け算が+1のものを、ポジティブフィードバックと呼ぶ。 - 11.ネガティブフィードバック
上と同様に、サイクルを一周したときの数字の掛け算がー1のものを、ポジティブフィードバックと呼ぶ。
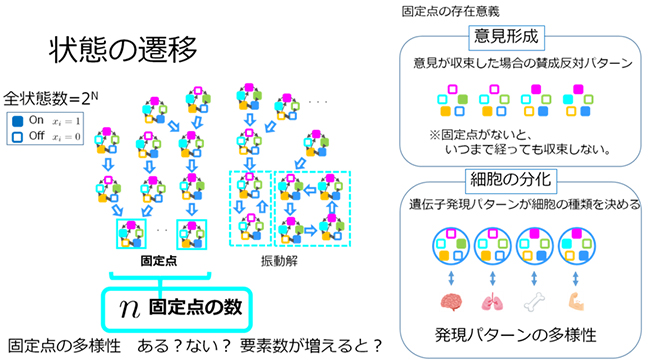
図1 ブーリアンネットワークの状態遷移と固定点の存在意義
左)赤、水色、黄、青、緑の四角が各要素、各要素間の黒矢印がリンクで、つながった五角形がブーリアンネットワークである。系全体の状態は、ある初期状態から出発すると、それ以上は状態が変わらない固定点(水色線で囲んだ状態)か、状態が周期的に変わる振動解(水色の破線で囲んだ状態)のどちらかに行き着く。
右)上の意見形成プロセスモデルでは、固定点が存在しないことはいつまでたっても意見を決められない人が必ずいることを意味する。下の細胞の分化モデルでは、固定点に対応する遺伝子発現パターンが細胞の種類を決定しているので、細胞の種類に多様性が存在するためには、系が多くの固定点を持つ必要がある。(固定点でなく、振動解と対応しているという説もある。)
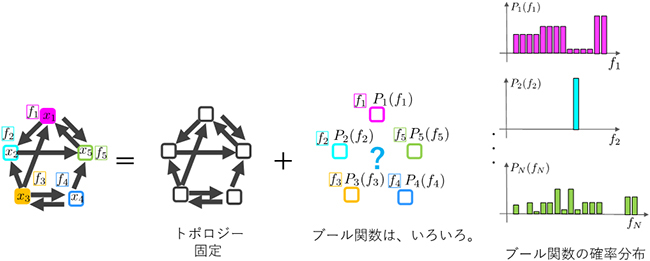
図2 ブーリアンネットワークのブール関数を確率分布に従って割り振る概念図
系のネットワークのつながり方(トポロジー)を固定し、各要素に与えるブール関数を決めると、固定点の数は一意に決まる。ここでは、ブール関数をさまざまな確率分布に従って割り振ると仮定して、固定点の数の平均を考える。
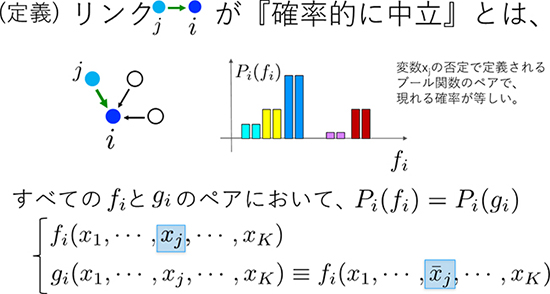
図3 確率中立の定義
あるリンクが確率的に中立のとき、そのリンクが活性の役割を果たす確率と、抑制の役割を果たす確率は等しい。活性・抑制と定まらないブール関数のペアでも、現れる確率は等しい。
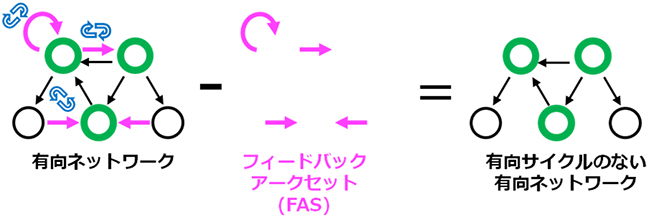
図4 フィードバックアークセット(FAS)の説明図
フィードバックアークセットとは、それを取り除くとネットワークから有向サイクルが消失するリンクの集合で定義される。左の有向ネットワークには有向サイクル(青い矢印のサイクル)が3つ存在するが、ピンクの太いリンク(矢印)を取り除くと、右のような有向サイクルのない有向ネットワークとなる。
