理化学研究所(理研)脳神経科学研究センター統計数理研究ユニットの松⽥孟留ユニットリーダーらの国際共同研究チームは、データをもとに未知の量を推定する統計学の問題において、ベクトル[1]の推定で知られている古典的な結果を行列[2]の推定に一般化しました。
本研究成果は、データの背後に潜む構造を捉えて解析する統計手法の開発に貢献すると期待できます。
データをもとに未知の量を推定することは統計学の基本的な問題であり、さまざまな推定方法が研究されています。ベクトルの推定において、標準的な推定方法である最尤(さいゆう)推定[3]よりも精度の良い「縮小推定[4]」という方法が知られています。一方で、複数の変数を同時に解析する状況では未知の量が行列の構造を持ちますが、行列の縮小推定についてはベクトルに比べて未解明な点が多く残されています。
今回、国際共同研究チームは「行列二乗損失[5]」と「行列優調和性[6]」という数学的概念を導入することで行列の縮小推定の理論を整備し、ベクトルの場合に知られている古典的な結果を一般化しました。さらに、最尤推定よりも精度の良いベイズ推定[7]の方法を開発し、この方法によってデータの持つ低ランク性[8]という性質を生かした推定が行えることを数値実験で示しました。
本研究は、統計学の雑誌『Biometrika』オンライン版(8月2日付:日本時間8月2日)に掲載されます。
背景
統計学では、データが確率的に生成されるという仮定のもと、データが従う確率分布を正規分布やポアソン分布などの統計モデルによって表現します。統計モデルには平均や分散(ばらつき)などを表す未知のパラメータが含まれており、これをデータから推定するのは統計学の基本的な問題です(図1)。推定方法としては、手元のデータを生成する確率(尤度)を最大にする最尤(さいゆう)推定や、ベイズ統計学の考え方に基づいたベイズ推定などがあります。
1956年、統計学者のCharles Steinは多変量正規分布の平均ベクトルの推定において、3次元以上では、最尤推定よりも推定精度が良い(平均二乗誤差[9]が小さい)推定方法が存在することを示しました。これは直感と反する現象であるため「Steinのパラドックス」と呼ばれています。最尤推定より推定精度が良い推定方法として、「縮小推定」という方法が知られています。また、Steinは優調和な事前分布[10]を用いたベイズ推定は、最尤推定より推定精度が良いことも示しました。
縮小推定はベクトルだけでなく行列にも有効です。現実のデータでは、大きいサイズの行列が小さいサイズの行列の積でよく近似できることが多く、このような性質を「低ランク性」といいます。そこで、低ランク性のもとで良い推定精度を発揮する縮小推定の方法が開発されました。これは行列の空間の数学的構造を生かした推定方法といえます。一方で、推定方法の比較基準については、これまでの研究のほとんどはベクトルと同様に平均二乗誤差を用いており、行列の空間の数学的構造を考慮したものになっていませんでした。
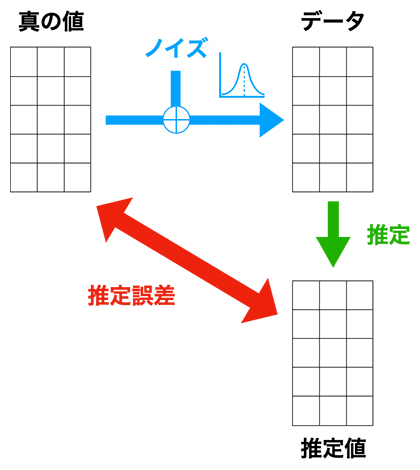
図1 行列推定の問題設定
統計学ではデータには確率的なノイズが含まれていると仮定する。本研究では、正規分布に従うノイズが加わった行列データ(右上)から、真の行列を推定する問題を考えた。真の値と推定値のずれである推定誤差が小さい推定方法が望ましい。
研究手法と成果
国際共同研究チームはまず、行列の空間の数学的構造を考慮した「行列二乗損失」という比較基準に着目しました。例えば、あるクラスで行った試験の点数のデータをもとに、各生徒の総合学力を推定することを考えましょう。ここで、総合学力とは各科目の能力の重み付き和(係数をかけて作られる和)とします。このとき、推定方法Aが推定方法Bを行列二乗損失のもとで上回るならば、どんな重みを用いる場合でも、推定方法Aの方が推定方法Bよりも総合学力の推定精度が良い(平均二乗誤差が小さい)ことになります。このように、行列二乗損失は複数の変数を同時に解析する状況で有用な比較基準になっています。
次に、「行列優調和性」という数学的概念を導入し、行列優調和関数が優調和関数[11]と類似した性質を持つことを証明しました。例えば、優調和関数がラプラシアン[12]を用いて特徴付けられることに対応して、行列優調和関数が行列版のラプラシアンによって特徴付けられることを示しました。そして、行列優調和な事前分布を用いたベイズ推定が最尤推定を行列二乗損失のもとで上回ることを証明しました。これはベクトルの縮小推定に関するSteinの結果の行列への一般化になっています。
さらに、規格化できない(improper)行列t分布(図2上)という分布が行列優調和となる条件を導出しました。この結果から、松田孟留ユニットリーダーらが2015年に発見した特異値縮小型事前分布(図2下)という分布注1)が行列優調和であることも導かれます。これらの事前分布を用いたベイズ推定は、低ランク行列の空間への縮小推定と解釈できます。また、ベクトルの縮小推定の方法をそのまま行列に適用すると、平均二乗誤差は最尤推定より小さいものの、行列二乗損失のもとでは最尤推定を上回らないことを証明しました。
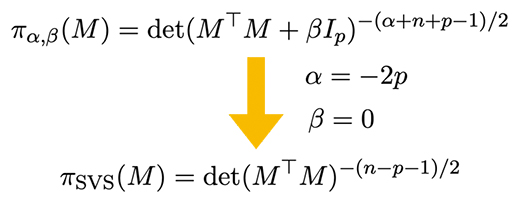
図2 行列t分布(上)と特異値縮小型事前分布(下)
t検定の基礎にもなっているt分布を行列に拡張したのが行列t分布である。本研究では、行列t分布が行列優調和になるαとβの範囲を導出した。特異値縮小型事前分布(Steinの事前分布の一般化)はこの範囲に含まれている。
最後に、数値実験によって理論結果の妥当性を検証しました。行列優調和な事前分布を用いたベイズ推定が最尤推定を上回り、特に低ランクの状況で良い推定精度を発揮することが確認されました(図3)。また、行列優調和性に基づいた推定方法は高次元データに対してより効果的であることも分かりました。
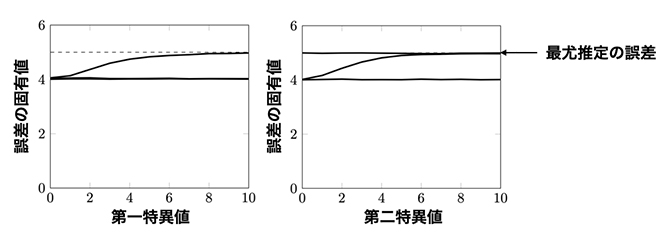
図3 行列優調和な事前分布を用いたベイズ推定の推定精度
5行3列の行列の推定における行列二乗リスク(行列二乗損失の平均)の三つの固有値のプロット。左はランク1、右はランク2の場合。特異値の値によらず安定して推定精度が良いことが分かる。
- 注1)T. Matsuda and F. Komaki. Singular value shrinkage priors for Bayesian prediction. Biometrika, 102, 843--854, 2015.
今後の期待
ベクトルの縮小推定に関する理論は、多くの統計手法の土台になっているため、本研究の成果が新たな統計手法の開発につながることが期待されます。特に、近年さまざまな分野で高次元データが得られるようになりましたが、こうした高次元データには低ランク性が潜んでいることも多く、本研究の着想が有効だと考えられます。
行列をさらに一般化した量としてテンソル[13]があります。テンソルの解析は数学的に困難な点が多いですが、本研究の成果をもとにしてテンソルの縮小推定の理論についても手がかりが得られることが期待できます。また、本研究で導入した行列優調和性の概念を用いることで、行列の空間に関する理解が進むかもしれません。
補足説明
- 1.ベクトル
数字を縦に一列に並べたもの。 - 2.行列
数字を縦と横に矩形状に並べたもの。線形代数という数学の分野で研究されている。 - 3.最尤(さいゆう)推定
手元のデータを生成する確率(尤度)を最大にするパラメータを推定値とする推定方法。さまざまな観点から良い性質を持つことが知られている。 - 4.縮小推定
パラメータ空間の何らかの部分集合に向けて推定値を引き寄せる(縮小する)推定方法。パラメータの真の値が縮小先の部分集合に近いときに良い推定精度を発揮する。 - 5.行列二乗損失
行列の推定方法を比較するための基準。推定方法Aが推定方法Bを行列二乗損失のもとで上回るならば、どんな重みを用いる場合でも、推定方法Aの方が推定方法Bよりも列ベクトルの重み付き和の推定精度が良い(平均二乗誤差が小さい)。 - 6.行列優調和性
関数の優調和性という性質を行列変数の関数に拡張したもの。行列版のラプラシアンで特徴付けられる。 - 7.ベイズ推定
ベイズ統計学の考え方に基づいた推定方法。ベイズ統計学とは、パラメータに事前分布という確率分布を設定し、ベイズの公式によってデータと統合することで柔軟なデータ解析を可能とする統計学の枠組みである。 - 8.低ランク性
大きいサイズの行列が小さいサイズの行列の積で良く近似できること。現実のデータでしばしば現れる。 - 9.平均二乗誤差
推定誤差(真の値と推定値の差)の二乗の平均値。小さいほど推定精度が良い。 - 10.事前分布
ベイズ統計学でパラメータに関する事前知識を表現する確率分布。本研究では、推定精度の良いベイズ推定を行うための事前分布について考えた。 - 11.優調和関数
ラプラシアンがゼロ以下である関数(より正確な定義は論文を参照)。ポテンシャル論という数学の分野で研究されている。 - 12.ラプラシアン
多変数関数の各変数に関する二階微分を足し合わせたもの。統計学だけでなく物理学でもよく現れる。 - 13.テンソル
数字をルービックキューブのように三次元に並べたもの。例えば、あるクラスで1年間に行った期末試験の点数のデータは、生徒×科目×学期のテンソルで表現される。より高次元のテンソルも考えることができる。
国際共同研究チーム
理化学研究所 脳神経科学研究センター 統計数理研究ユニット
ユニットリーダー 松田 孟留(まつだ たける)
ラトガース大学 統計学部
教授 ウィリアム・ストロダーマン(William Strawderman)
研究支援
本研究は、日本学術振興会(JSPS)科学研究費若手研究「多様な時系列データに潜む振動現象の統計解析(領域代表者:松田孟留)」による支援を受けて行われました。
原論文情報
- Takeru Matsuda, William E. Strawderman, "Estimation under matrix quadratic loss and matrix superharmonicity", Biometrika, 10.1093/biomet/asab025
発表者
理化学研究所
脳神経科学研究センター 統計数理研究ユニット
ユニットリーダー 松田 孟留(まつだ たける)
報道担当
理化学研究所 広報室 報道担当
お問い合わせフォーム
