ポイント
- 大きくスピン分裂した電子スピン偏極フェルミ面の量子振動を観測
- 量子振動の解析により3次元物質で初めて電子スピンのベリー位相を検出
- 電子スピンのトポロジー情報が位相値に反映されていることを実証
要旨
理化学研究所(理研、野依良治理事長)は、極性を持つ(上下の反転対称性が破れた)3次元の半導体物質「BiTeI(Bi:ビスマスTe:テルル I:ヨウ素、図1)を使い、3次元物質における電子スピンのベリー位相[1]の検出に初めて成功しました。これは、理研創発物性科学研究センター(十倉好紀センター長)強相関量子伝導研究チームのハロルド・ファンチームリーダー、村川寛客員研究員、強相関理論研究グループの永長直人グループディレクター、モハマド・サイード・バーラミー客員研究員、強相関物性研究グループの十倉好紀グループディレクター、金子良夫上級技師、東京大学国際超強磁場科学研究施設徳永将史准教授、小濱芳允特任助教、スタンフォード大学のクリスベル助教との共同研究グループによる成果です。
電子スピンのベリー位相は、時間的に変化する通常の量子力学的位相とは異なり、量子空間での電子スピンの幾何学的性質によって決まります。この位相は身のまわりのさまざまな量子現象を支配する普遍的な存在であり、物性を理解するための重要な情報を含んでいます。しかし、ベリー位相の実験的な検出は容易ではなく、定量的な評価にも多くの問題点が残されたままでした。
共同研究グループは、結晶構造に極性を持つ3次元の半導体BiTeI単結晶の磁気抵抗率の量子振動[2](電気抵抗率が磁場の関数として振動する)を測定しました(図2)。その結果、スピン軌道相互作用[3]によって電子の運動方向とスピンの向きが連動する「ラシュバ型電子スピン構造[4]」(図3)が持つベリー位相の検出に成功しました。この物質固有の非常に大きな電子スピン分裂エネルギー[5]による電子スピン偏極[6]で、環状のラシュバ型電子スピン構造が強磁場中でも安定して存在するため、量子振動の解析からスピン構造の幾何学性により定まるベリー位相値を実験的に検証することができました。
ベリー位相の定量的な解析によって物質中の電子スピンの振る舞いを読み解くことが可能になれば、多様な物性の理解が進み、新しい量子現象の開拓やスピントロニクス分野への応用につながるものと期待されます。
本研究成果は、米国の科学雑誌『Science』(12月20日号)に掲載されるに先立ち、オンライン版(12月19日付け:日本時間12月20日)に掲載されます。
背景
量子力学で、状態空間の幾何学的性質によって定まるベリー位相は普遍的な概念です。物質中の電子波動関数[7]に含まれるベリー位相は、物質を理解するために重要な情報が含まれており、身の周りのさまざまな量子現象と密接に関わっています。最近では、電子スピンが作り出す渦やねじれなどの幾何学的構造(電子スピンのトポロジー[8])が生み出す現象の潜在性が理論的にも応用的にも広く注目されており、電子スピン由来のベリー位相の研究が盛んに行われています。しかし、その実験的な検出は容易ではなく、定量的な評価にも多くの問題点が残されたままでした。
研究手法と成果
共同研究グループは、極性半導体BiTeI単結晶のシュブニコフ・ドハース(SdH)振動[9](電気抵抗率が磁場の関数として振動する)を測定し、3次元物質のラシュバ型スピン構造が持つベリー位相の検出に成功しました(図2)。スピン方向に依存した電子状態のエネルギー分裂により、内側と外側に2つのフェルミ面[10]が形成され、それぞれ回転方向が逆の環状スピン構造が現れます(図3)。環状スピンの幾何学性により、ベリー位相値はπ(= 180 ˚)となる(量子振動が反転する)ことが理論的に予想されていましたが、今回これを実験的に証明することができました。
SdH振動測定によるピーク位置の解析(図2)はベリー位相の評価に使われる一般的な手法です。従来のラシュバ型物質ではそのスピン分裂エネルギーが小さく、2つのスピン偏極フェルミ面の大きさ(図3でそれぞれの環状スピンの囲む面積)に顕著な差が現れないため、それぞれの電子状態のSdH振動を解析可能な形で分離できませんでした。重元素で構成されるBiTeIではスピン軌道相互作用がとても強く、3次元の極性構造中で巨大なスピン分裂エネルギーが発生するため2つのスピン偏極フェルミ面の大きさに明確な差が現れます。その結果、それぞれのフェルミ面由来のSdH振動を完全に分離して位相値を解析できることに加え、強磁場中でもラシュバ型環状スピン構造が安定して存在する(スピンを磁場方向に平行にそろえるゼーマンエネルギーよりもラシュバ型スピン分裂エネルギーの方がはるかに大きい)ことから、ベリー位相を定量的に求めることが可能となりました。
今後の期待
今回の研究では、電子スピンのベリー位相の存在を明らかにするとともに、その値が電子スピンのトポロジーの情報を如実に反映していることを示しました。ベリー位相の定量解析によって電子スピン状態を読み解くことが可能となれば、電子スピンのトポロジーが絡んだ多様な物性の理解に向けて大きく前進するものと期待されます。
なお、本研究の一部は最先端研究開発支援プログラム(FIRST)により日本学術振興会を通して助成されたものです。
原論文情報
- H. Murakawa、M. S. Bahramy、M. Tokunaga、Y. Kohama、C. Bell、Y. Kaneko、N. Nagaosa、Harold Y. Hwang、Y. Tokura“Detection of Berry’s Phase in a Bulk Rashba Semiconductor” Science, 10.1126/science.1242247
発表者
理化学研究所
創発物性科学研究センター 強相関物理部門 強相関量子伝導研究チーム
客員研究員 村川 寛 (むらかわ ひろし)
(現在勤務先 大阪大学大学院理学研究科物理学専攻)
お問い合わせ先
創発物性科学研究推進室
Tel: 048-467-9258 / Fax: 048-467-8048
報道担当
理化学研究所 広報室 報道担当
Tel: 048-467-9272 / Fax: 048-462-4715
「最先端研究開発支援プログラム」に関するお問い合わせ先
独立行政法人 日本学術振興会
研究事業部 最先端研究助成課 最先端助成係
Tel: 03-3263-1698
first [at] jsps.go.jp
※[at]は@に置き換えてください。
研究課題「強相関量子科学」支援全般に関わるお問い合わせ先
独立行政法人理化学研究所
創発物性科学研究センター 強相関量子科学研究支援チーム
チームリーダー 平林 泉 (ひらばやし いずみ)
Tel: 048-462-4660
補足説明
- 1.電子スピンのベリー位相
運動量(波数)空間内での電子スピンの幾何学的性質によって一意的に定まる量子力学的位相。時間的に変化する通常の位相とは区別される。 - 2.量子振動
磁場中で量子化された最大エネルギー準位の電子占有率は、磁場の値の逆数に対して周期的に変化する。このため、磁化などの物理量には電子状態の変化を反映して磁場の逆数に対する周期的な振動が観測される。その周期は磁場に対して垂直なフェルミ面の断面積と関係しているため、BiTeIのように大きくエネルギー分裂したフェルミ面の断面積に顕著な差があるときには、それぞれのフェルミ面に属する電子からの量子振動を分離して観測できる。 - 3.スピン軌道相互作用
運動中の電子が周辺の荷電粒子の相対的な運動(電子から見た電流)による実効的な磁場を感じ、そのスピン方向が運動方向(軌道)に対して特定の方向に固定されること。BiTeIのような極性構造を持つ物質中を運動する電子では、運動方向と垂直な一方向に実効的な磁場を感じるため、 図3のようなスピン構造が現れる。 - 4.ラシュバ型電子スピン構造
スピン軌道相互作用により運動方向に対して垂直な左右の一方向に電子スピンが固定されている状態。波数空間で見ると 図3のようにスピン分裂した環状のスピン構造が現れる。 - 5.電子スピン分裂エネルギー
電子スピンが反転した状態間のエネルギー差。本物質では、スピン軌道相互作用により電子の運動方向に対して右向きスピンと左向きスピンの電子状態のエネルギーレベルが大きく分裂する。 - 6.電子スピン偏極
上下、又は左右2つのスピン方向のどちらかの状態が選択的に存在する状態。ここでは“電子の運動方向に対して”電子スピンが左右のどちらかに固定されている状態。 - 7.電子波動関数
電子の量子力学的状態を特徴づける振幅と位相で表現される関数。振幅は電子の存在確率に関係し、位相はエネルギーや運動量、さらに系の状態を特徴づける物理量の幾何学的性質の情報を含む。 - 8.電子スピンのトポロジー
波数空間において電子スピンが形成する渦やねじれなどの幾何学的構造。 - 9.シュブニコフ・ドハース振動
電気抵抗率に見られる量子振動のこと。 - 10.フェルミ面
フェルミ粒子である電子は同じ運動状態を取ることができないため、波数空間においてエネルギーの低い状態から順番に占有されていく。そのように電子を詰めて行ったときの最も外側の等エネルギー面のこと。又は波数空間において電子が占める部分の表面。
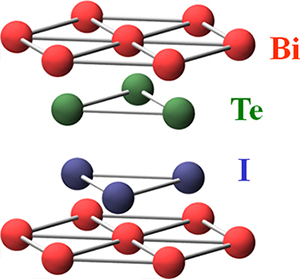
図1 BiTeIの結晶構造
Bi、Te、I原子がそれぞれ三角格子を形成し、それらが順番に積層している。このため積層方向に対して反転対称性が破れた極性構造を取る。さらに、結晶を構成する重元素による強いスピン軌道相互作用が加わることで、大きなラシュバ効果が3次元で実現している。
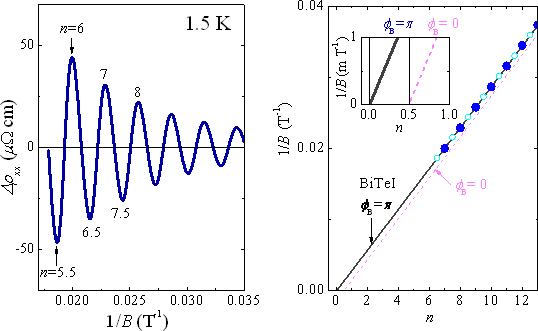
図2 量子振動の解析によるベリー位相の評価
- (左図)BiTeIのシュブニコフ・ドハース振動成分。磁場の逆数に対して電気抵抗率が周期的に振動する。
- (右図)電気抵抗率の極大値を整数、極小値を半整数として左図のように指数付けし、磁場の値の逆数に対する線形性を外挿した切片が0となっており、ベリー位相(φB)の値がπとなることを示している。ベリー位相値がゼロ(φB = 0)の通常の金属では点線のように1/2の切片を取る。
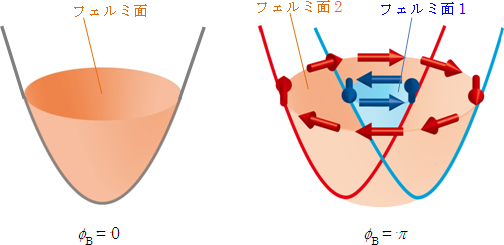
図3 波数空間における電子エネルギー状態
通常の金属(左)では電子スピン方向はエネルギー縮退しておりベリー位相φB = 0であるが、ラシュバ型スピン分裂状態(右)では電子スピンが運動方向に対して一方の垂直方向に固定されて環状の電子スピン構造が実現する。スピン方向によってエネルギー分裂した状態では、それぞれ逆まわりの環状スピンで囲まれた2種類のフェルミ面が存在する。スピン分裂した電子状態のベリー位相値はπとなることが理論的に示されている。
