要旨
理化学研究所(理研)理論科学連携研究推進グループ分野横断型計算科学連携研究チームの横倉祐貴基礎科学特別研究員と京都大学大学院理学研究科物理学宇宙物理学専攻の佐々真一教授の共同研究チームは、物質を構成する粒子の“乱雑さ”を決める時間の対称性[1]を発見しました。
乱雑さは、「エントロピー[2]」と呼ばれる量によって表わされます。エントロピーはマクロな物質の性質をつかさどる量として19世紀中頃に見い出され、その後、さまざまな分野に広がりました。20世紀初頭には、物理学者のボルツマン、ギブス、アインシュタインらの理論を踏まえて「多数のミクロな粒子を含んだ断熱容器の体積が非常にゆっくり変化する場合、乱雑さは一定に保たれ、エントロピーは変化しない」という性質が議論されました。同じ頃、数学者のネーターによって「対称性がある場合、時間変化のもとで一定に保たれる量(保存量)が存在する」という定理が証明されました。
20世紀末、ブラックホール[3]のエントロピーは、時空の対称性から導出できることが分かりました。この研究に触発され、今回、共同研究チームは、「ネーターの定理に従って保存量としてのエントロピーを導く対称性は何か?」という疑問を追究しました。具体的には、「ミクロな粒子の運動を記述する時間をずらしても、ずらす前の運動と同じ法則に従う」という対称性があるかを調べました。その結果、量子力学のプランク定数[4]を温度で割った分だけ時間をずらすように選んだときにのみ、そのような対称性が現れることが分かりました。そして、ネーターの定理をその対称性に適用することで得られる保存量がエントロピーと一致しました。この乱雑さを決める時間の対称性はこれまでにないものであり、どのような物質にも現れうる普遍的なものです。
今後、時間の対称性が導くエントロピーは、乱雑さとしてのエントロピーとは異なる方法でミクロとマクロの世界を結び付けることを可能にし、さまざまな分野に新しい視点を与えると期待できます。
本研究は、米国の科学雑誌『Physical Review Letters』(4月8日号)に掲載され、Editors’ suggestionに選ばれました。
背景
およそ100年前、熱力学の基本的な量であるエントロピーのミクロな力学による表現が確立され、また、力学における対称性と保存則を一般的に結び付ける数学的定理が発見されました。前者はボルツマンの公式、後者はネーターの定理と呼ばれます。
熱力学とは、マクロな物質の性質を体系的に記述する学問です。19世紀中頃、エントロピーは、熱的現象と力学的現象を結び付ける量としてクラウジウスにより見出されました。熱力学によれば、断熱容器の体積が非常にゆっくり変化する場合、その中に入れられた物質のエントロピーは変化しません。19世紀末、ボルツマンは、マクロな物質のエントロピーを、物質を構成するミクロな粒子の乱雑さとして表現しました(ボルツマンの公式)。これにより、マクロな物質の熱力学とミクロな力学の世界が結び付きました。そして、20世紀初頭、このボルツマンの表現としてのエントロピーが断熱下のゆっくりした変化で保たれることが議論されました。
一方、自然界にはさまざまな「対称性」が存在します。20世紀初頭に、数学者のネーターは「対称性がある場合、時間変化のもとで一定に保たれる量(保存量)が存在する」という定理を示しました。ここで、「対称性がある」とは、「ある運動法則に従う粒子の軌道を、ある規則に従って移動させると、再び同じ運動法則に従う」ことを意味します。ネーターの定理は、現代物理学における基本的かつ重要な考え方になっています。
今回、共同研究チームは、上記のようにエントロピーが断熱下のゆっくりした変化で保存されることから「ネーターの定理に従って保存量としてのエントロピーを導く対称性は何か?」という疑問を持ち、その解明を試みました。これに対する解答によって、ボルツマンの公式とネーターの定理が結ばれることになります。
実は、この疑問はブラックホールの研究に触発されたものです。20世紀末、ブラックホールのエントロピーは、時空の対称性から導き出せることが分かりました。ブラックホールのエントロピーと物質のエントロピーの関係は、まだ明らかになっていません。しかし、「ブラックホールのエントロピーが対称性から導かれるなら、物質のエントロピーも同じではないか?」という発想がこの疑問につながりました。
研究手法と成果
まず、エントロピーがどのように保存されるのかを簡単にみてみましょう。多数のミクロな粒子をピストンのついた断熱容器に入れ、ピストンをゆっくり押して容器の体積を小さくさせたとします。すると、容器の外から仕事をされ、粒子のエネルギーが増えます。その結果、粒子の運動が激しくなり乱雑さが増加します。ところが、同時に、粒子が移動できる範囲が狭くなる分だけ乱雑さが減少します。このように両者の寄与が打ち消し合うため、乱雑さは保たれます。つまり、エントロピーが保存されます。
共同研究チームは、ネーターの定理に従ってこのエントロピーの保存則を導く対称性を探そうと考えました。そこで、エントロピーの保存則が断熱下のゆっくりした変化でのみ成立することに注目し、「物質を構成する粒子の運動が、マクロな物質の熱力学量のゆっくりとした時間変化に対応する条件」を数式として書き出しました。これが鍵となり、マクロな熱力学の時間変化とミクロな力学の時間変化が結び付きました。
実際、その条件を満たすミクロな運動に限った場合にのみ、時間に対する特別な対称性が現れることが分かりました。具体的には、「ミクロな粒子の運動を記述する時間をずらしても、ずらす前の運動と同じ法則に従う」という対称性があるかどうかを調べました。その結果、量子力学のプランク定数を温度で割った分だけ、時間をずらすように選んだときにのみ、そのような対称性が現れました。そして、ネーターの定理をその対称性に適用することで得られる保存量がエントロピーと一致しました。ここでの温度はボルツマンの公式によって決まる量であり、時間に依存して変化します(図)。
これは、これまでにない対称性の発見であり、どのような物質にも現れうる普遍的なものです。ここで興味深いのが、この理論は完全に古典論に基づくにもかかわらず、プランク定数の存在が自然と導かれた点です。これは、エントロピーと量子力学の深い関係を示していると考えられます。
今後の期待
この対称性の物理的な描像はまだ明らかではありません。しかし、それが理解できれば、これまでの乱雑さとしてのエントロピーとは異なる方法で、ミクロとマクロの世界を結び付けることが可能になり、さまざまな分野に新しい視点を与えることが期待できます。
1つの可能性は、ブラックホールのエントロピーの微視的起源の理解です。ブラックホールのエントロピーを導く時空の対称性と今回得られた対称性は似ていますが、2つの関係は分かっていません。得られた対称性をより深く理解し、時空の対称性との関係を見出すことができれば、時空の微視的構造に対する研究の突破口になるかもしれません。
もう1つの可能性は、時間の矢[5]の問題です。一般には、ピストンをどのように動かしても乱雑さを減少させることはできず、エントロピーは決して減少しません。これは熱力学第二法則と呼ばれ、エントロピーが増大する向きにのみ状態が変化することを意味します。つまり、時間の向きとエントロピーの増大する向きが対応します。これをミクロな立場から理解するのに、今回の対称性の視点が役立つ可能性があります。
原論文情報
- Shin-ichi Sasa and Yuki Yokokura, "Thermodynamic Entropy as a Noether Invariant", Physical Review Letters, doi: 10.1103/PhysRevLett.116.140601
発表者
理化学研究所
研究推進グループ 理論科学連携研究推進グループ (iTHES) 分野横断型計算科学連携研究チーム
基礎科学特別研究員 横倉 祐貴 (よこくら ゆうき)
京都大学大学院理学研究科物理学宇宙物理学専攻
教授 佐々 真一 (ささ しんいち)
報道担当
理化学研究所 広報室 報道担当
Tel: 048-467-9272 / Fax: 048-462-4715
京都大学企画・情報部広報課国際広報室
Tel: 075-753-5729 / Fax: 075-753-2094
comms [at] mail2.adm.kyoto-u.ac.jp(※[at]は@に置き換えてください。)
補足説明
- 1.対称性
ある運動法則に従う粒子の軌道に、ある変換を施すとする。もし変換後の軌道が前と同じ運動法則に従うならば、「その運動法則はその変換に対して対称性がある」という。例えば、摩擦のない平坦な床にボールを転がすと、等速直線運動という軌道を描く。今度は、先ほどとは異なるところから転がすと、再び等速直線運動をする。これは、床の均一性という対称性を表し、「空間並進対称性」と呼ばれる。この対称性に対応して、ネーターの定理により運動量が保存される。 - 2.エントロピー
熱力学において物質の状態を表す量の1つ。物質を構成する粒子の乱雑さを表わす。温度が一定に保たれたままゆっくり変化する場合には、受け取る熱を温度で割った量が変化する前と後でのエントロピーの差となる。断熱されたままゆっくり変化する場合にはエントロピーは一定の値をとる。以上の熱測定によってエントロピーを決定できる。 - 3.ブラックホール
重たい星の寿命の最後に形成されうる、重力の非常に強い領域のこと。一般相対性理論では、重力は時空の幾何学で表現されるため、ブラックホールは極端に曲がった時空だと言える。20世紀後半にホーキングは、「量子力学の効果により、ブラックホールは温度とエントロピーを持つ」ことを示した。興味深いことに、そのエントロピーは通常の物質と異なり、体積ではなく表面積に比例している。そのミクロな乱雑さの起源はまだ分かっていないが、時空の微視的構造に関係するため、多くの研究者がこの問題に取り組んでいる。 - 4.プランク定数
物理学における基本定数の1つ。量子論においてエネルギーと振動数を結びつける普遍的な比例係数として定義され、量子力学的な振る舞いを特徴付ける。hと記され、h=6.6 x 10-34ジュール秒という値を持つ。 - 5.時間の矢
熱い湯と冷たい水を混ぜると自然にぬるま湯になるが、ぬるま湯が湯と水に分かれることはない。このように、時間には向きがあり、それを「時間の矢」という。
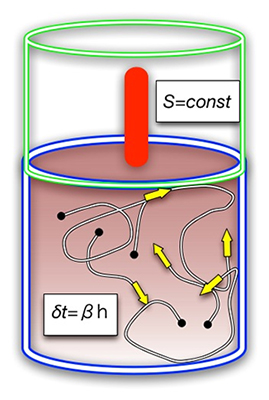
図 エントロピーを導く時間の対称性の概念図
黒丸は断熱容器に入れられた物質を構成する粒子、ひものようなものは粒子の軌跡を表す。Sはエントロピー、βは温度の逆数、hはプランク定数を表す。ピストン(赤)によって断熱容器の体積をゆっくり変化させると、エネルギーは変化するが、エントロピーは一定に保たれる(S=const)。ミクロな力学において、時間をδt=βhだけずらしても運動の法則は変わらない。ネーターの定理より、この対称性に対する保存量がエントロピーを与える。
