理化学研究所(理研)創発物性科学研究センター計算量子物性研究チームの関和弘研究員と柚木清司チームリーダー(計算科学研究センター量子系物質科学研究チームチームリーダー、開拓研究本部柚木計算物性物理研究室主任研究員)の研究チームは、行列のべき乗[1]を量子コンピュータ[2]上で計算する効率的な量子アルゴリズムを提案しました。
本研究成果は、将来実用が期待されている量子コンピュータを用いて量子多体問題を数値的に解くための有用な量子アルゴリズムになると期待できます。
今回、研究チームは、数値線形代数でその有用性がよく知られている行列のべき乗算を、量子コンピュータを用いて行う量子アルゴリズムを提案しました。行列のべき乗をそのまま量子コンピュータで計算しようとすると、計算する項の数が量子ビット[2]の数に対して指数[1]関数的に増加するためその計算は難しくなります。そこで、量子ダイナミクスを決める時間発展演算子[3]の線型結合を利用するというアイデアをもとに、行列のべき乗を制御された誤差の範囲で効率的に計算する今回の提案に至りました。提案した量子アルゴリズムの応用として、クリロフ部分空間法[4]を用いた量子多体系[5]のハミルトニアン[6]の基底状態エネルギー[7]計算の数値シミュレーション実行例も示しました。
本研究は、科学雑誌『PRX Quantum』オンライン版(2月26日付)に掲載されました。
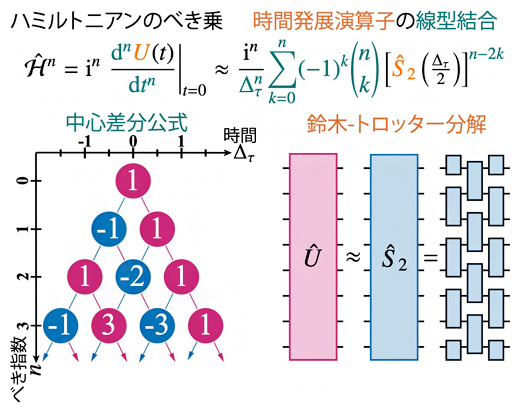
提案した量子アルゴリズムの概略図
背景
数値計算による量子多体系の解析は、物性物理学や量子化学などにおける難問への最も有用なアプローチの一つです。通常のコンピュータ[8]を用いた数値線形代数で知られているべき乗法の考え方、つまり適切に用意したベクトルに対して行列を繰り返し乗算する技法は、量子多体系の基底状態やダイナミクス計算に利用されるさまざまな計算手法の基本的な要素となっています。
ただし、量子多体系では、量子状態やハミルトニアンを表現するベクトルや行列の次元が、その構成要素の数Nに関して指数関数的に大きくなります。例えば、S=1/2スピン[9]がN個ある量子多体系の任意の量子状態を表現するには、2N次元のベクトル[10]が必要です。このため、量子多体系の計算を通常のコンピュータで行う場合、その計算量はNに関して指数関数的に増大します。これが、大きなNを持つ量子多体系の計算が通常のコンピュータで難しい理由です。
物性物理学や量子化学の分野では、量子状態を表す2N個全てのベクトル要素を保持せずに通常のコンピュータ上で計算する手法も発展しています。しかしそのような手法を用いた場合でも、ハミルトニアンのべき乗を展開した項の数がべき指数[1]に対して指数関数的に大きくなるため、大きなべき指数を持つハミルトニアンのべき乗を通常のコンピュータで計算することは一般に容易ではありません。
一方、N個の量子ビットを利用できる量子コンピュータでは、2N次元のベクトルに対する特定のユニタリ行列[11]の乗算を、量子回路[12]における1回の基本的な量子ゲート[12]操作で行い、任意のユニタリ行列の乗算は、基本的な量子ゲート操作の組み合わせで行います。また、計算結果の読み出しは、量子ビットの量子状態を適切に測定することで行います。このように、通常のコンピュータとは異なる動作原理で計算を行う量子コンピュータを活用し、通常のコンピュータでは困難な計算を効率的に行うための量子アルゴリズムの開発が、世界中で進められています。
研究手法と成果
まず、研究チームは、量子コンピュータによる量子状態の時間発展とその重ね合わせを利用して、ハミルトニアンのべき乗を計算する量子アルゴリズムを提案しました。これは、ハミルトニアンのべき乗を時間発展演算子の高階時間微分で表し、さらに時間微分を離散化した時間変数の差分で表すことで、ハミルトニアンのべき乗を時間発展演算子の線形結合で近似するという考えに基づいています。つまり、ハミルトニアンのべき乗をある量子状態に作用させた状態を、いくつかの異なる時間だけ時間発展させた量子状態の重ね合わせとして、制御された誤差の範囲で表すという仕組みになっています(図1)。
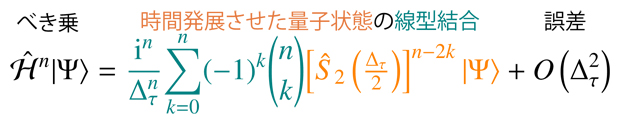
図1 提案したアルゴリズムのもとになる式
ハミルトニアンĤのn乗を量子状態|Ψ>に作用させた状態(左辺)を、n+1個の時間発展演算子(Ŝ2)を作用させた状態の線型結合(つまり重ね合わせ)で近似する(右辺第1項)。Δ_τは離散化した時間の単位で、離散化に伴う誤差の主要項はΔ_τの2乗に比例する(右辺第2項)。
この量子アルゴリズムでは、量子多体問題で登場する典型的なハミルトニアン[13]のべき乗の期待値計算を想定した場合、必要な量子ゲートの数が量子ビット数とべき指数に比例[14]し、測定の数は(べき指数+1)に比例します。つまり、少ない量子ゲート数で構成される量子回路に対する少ない回数の測定で計算できること意味しており、これは通常のコンピュータでは指数関数的な計算量が必要だったこととは対照的です。
また、近似として導入される時間変数の離散化による誤差は、離散化した時間での計算値の連続時間極限への外挿操作により系統的に消去できることを、解析計算と通常のコンピュータを用いた数値シミュレーションによって示しました(図2)。
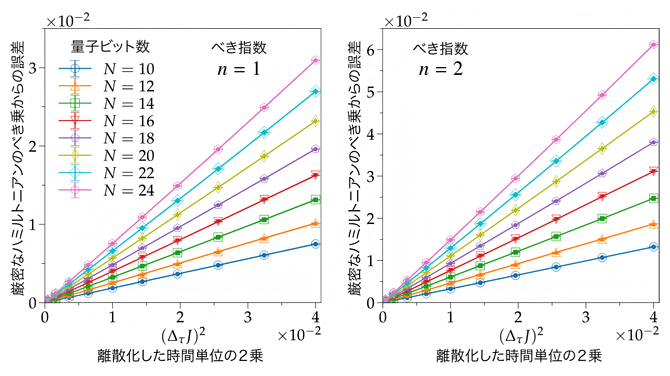
図2 提案した量子アルゴリズムで計算したハミルトニアンのべき乗に対する誤差の検証結果
提案した量子アルゴリズムで計算したハミルトニアンのべき乗の、厳密なハミルトニアンのべき乗からの誤差(演算子間の距離)を縦軸、離散化した時間単位Δ_τの2乗を横軸とし、左はべき指数がn=1の場合、右はべき指数がn=2の場合について、量子ビット数Nを10~24に変化させた数値シミュレーションの結果。ハミルトニアンとしては、反強磁性交換相互作用Jを有する1次元S=1/2ハイゼンベルク模型を用いている。べき指数や量子ビット数を変化させても、誤差は離散化した時間単位Δτの2乗にほぼ比例していることが分かる。べき指数nは100程度としても同様な結果が得られる。
さらに、提案したアルゴリズムをクリロフ部分空間法に応用して、ハイゼンベルク模型やハバード模型[15]の基底状態エネルギーを求める数値シミュレーションを通常のコンピュータを用いて行いました。数値シミュレーションでは、より少ないべき指数(つまりより少ない量子ゲート数)で精度の良い結果を得るには、対称性などの考察からなるべく基底状態に近い初期状態を選ぶことや、複数の初期状態を選ぶことが有効であることも示しました(図3)。少ない量子ゲート数で結果を得ることは、近い将来実用が期待されているノイズあり中規模量子(NISQ)コンピュータ[16]を用いて提案したアルゴリズムを実行するために特に大切な要素の一つです。
提案した手法は、基底状態エネルギー計算でよく用いられる他の量子アルゴリズム、変分量子固有値解法(VQE)[17]と異なり、変分パラメータの最適化が不要であり、また、量子回路の構成に任意性が少ない[18]という特徴があります。つまり、提案した量子アルゴリズムを使うと、他の量子アルゴリズムで現れた問題点を解消できる可能性があります。
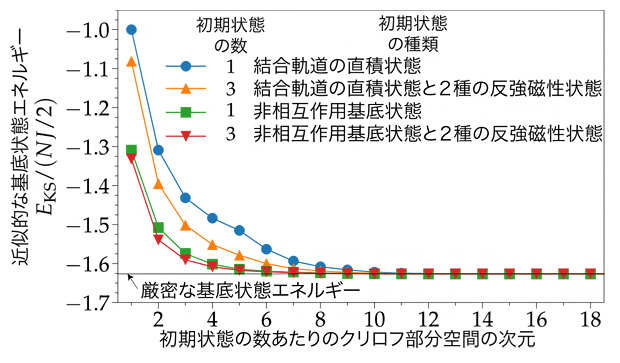
図3 ハバード模型の基底状態エネルギーの計算
提案した量子アルゴリズムを、図中に示した四つの初期状態を用いたクリロフ部分空間法による基底状態エネルギー計算に応用した結果。これらは、通常のコンピュータを用いたシミュレーションにより得た。縦軸は基底状態エネルギーEKS、横軸は初期状態の数あたりのクリロフ部分空間の次元。ハミルトニアンとしては、8格子点(N=16量子ビット)半充塡ハバード模型(ホッピングJに対する相互作用パラメータが4の場合)を用いた。横軸は、クリロフ部分空間の基底に現れるハミルトニアンの最大べき指数に1を加えたものに対応する。初期状態を工夫することで、より小さい初期状態の数あたりのクリロフ部分空間の次元(したがって、より少ない量子ゲート数)で、基底状態エネルギーに近い値を得られることが分かる。
今後の期待
今回、提案した量子アルゴリズムの検証は、量子ビット数Nの比較的小さな量子多体系について通常のコンピュータを用いた数値シミュレーションにより行いました。今後、量子コンピュータの性能が向上し、本研究で提案した量子アルゴリズムを量子コンピュータ上で実行できるようになった場合に、通常のコンピュータでは計算が困難なほどのNを持つ量子多体系について意味のある計算が実行できること、さらに、その結果、科学的に新たな知見が得られることが期待できます。
補足説明
- 1.行列のべき乗、指数、べき指数
正方行列Aと自然数nに対して、Aをn回かけ合わせた行列をAnと表し、行列Aのべき乗または累乗と呼ぶ。nのことを指数、もしくはべき指数と呼ぶ。 - 2.量子コンピュータ、量子ビット
量子ビットは量子力学的なビットのこと。通常のコンピュータにおける1ビットの状態は0か1のどちらかの値で記されるのに対して、量子コンピュータにおける1量子ビットの状態は0の状態と1の状態を重ね合わせた量子状態で記される。量子ビットを複数個用いることで、より大きな量子状態が表せる。量子ビットの量子状態は量子力学の法則に従って制御され、数学的には、複素数を成分とする有限次元の規格化されたベクトルで表現できる。量子状態を記す際には、|Ψ>や|Φ>といった記号がよく用いられる(ディラックの記法)。 - 3.時間発展演算子
量子状態の時間に関する変化を表す演算子。ある時刻における量子状態|Ψ>が、その時刻から時間がtだけ経過して量子状態Û(t)|Ψ>に変化するとき、Û(t)を時間発展演算子と呼ぶ。Û(t)はユニタリ演算子(内積を不変に保つ演算子)である。 - 4.クリロフ部分空間法
クリロフ部分空間に基づく数値線形代数の手法の総称。ベクトルxに行列Aのべき乗をかけて得られるベクトルの列x, Ax, A2x, …, Ak-1xが張る部分空間のことを、Aとxから生成されるk次のクリロフ部分空間と呼ぶ(kは自然数)。 - 5.量子多体系
量子力学に従い相互作用する多数の粒子から成る系。 - 6.ハミルトニアン
系のエネルギーに対応する演算子。量子多体系など量子系は、ハミルトニアンを与えることで定義される。Ĥをハミルトニアンとすると、時間発展演算子はÛ(t)=exp(-iĤt)と表される。ただし、expは指数関数、iは虚数単位、tは実数であり、Ĥは時間に依存しないと仮定した。またプランク定数は1とした。 - 7.基底状態エネルギー
ハミルトニアンの固有値のうち最も小さい固有値を基底状態エネルギーと呼び、対応する固有状態を基底状態と呼ぶ。 - 8.通常のコンピュータ
本稿では、量子コンピュータと区別するために、パソコンやスーパーコンピュータ(つまり、古典コンピュータ)のことを通常のコンピュータと呼ぶことにする。 - 9.S=1/2スピン
スピンは量子力学に登場する角運動量の一種で、その大きさSは非負の整数(0と正の整数)または半整数という離散的な値をとる。大きさSのスピンは2S+1通りの状態を取り得る。スピンは磁場や軌道角運動量と結合し、磁石の性質の起源となる。 - 10.2N次元のベクトル
S=1/2スピンは2通りの状態(アップとダウン)を取り得るので、N個のスピンのアップとダウンの配置としては2N通りがある。2N通りのアップとダウンの配置の量子状態たち(これらは一つの完全正規直交基底をなす)の重ね合わせで、N個のスピン系の任意の量子状態を記述できるが、その表現には重ね合わせの係数として2N個の複素数が必要となる。ここでの2N次元のベクトルとは、重ね合わせの係数であるこの2N個の複素数を成分に持つベクトルのこと。 - 11.ユニタリ行列
U†U=UU†=Iをみたす行列Uをユニタリ行列と呼ぶ。ただし、U†はUのエルミート共役(転置複素共役)で、Iは単位行列。 - 12.量子回路、量子ゲート
量子回路とは、どの量子ビットに対してどの量子ゲートをどのような順序で作用させ、どの量子ビットの状態を測定するかを定める図のことで、量子ビットと量子ゲートで構成される。量子ゲートは量子コンピュータにおいて、量子ビットを入出力とする演算のこと。量子ビットに量子ゲートを作用させることで、量子回路で表される量子状態を変化させる。 - 13.量子多体問題で登場する典型的なハミルトニアン
量子コンピュータで量子多体問題を扱うには、それを定義するハミルトニアンを量子ビット表示(パウリ演算子の積からなる項の和)に変換する。なお、量子ビット表示したハミルトニアンが最大でk個の量子ビットに作用する項を持つとき、その量子ビット表示のハミルトニアンをk局所ハミルトニアンと呼ぶ。量子ビット表示への変換の方法は唯一ではなく、kの値は変換の方法に依存する。 - 14.量子ビット数とべき指数に比例
項の数がN個程度のk局所ハミルトニアンによる時間発展演算子は、kN個程度の量子ゲート数で表現できる。k局所ハミルトニアンのn乗に対しては、時間発展演算子を最大でn回作用させるので、必要な量子ゲートの数はkNn個程度となる。本稿の本文の記述は、kの値は量子ビット数Nに対してO(1)の場合を仮定している。ここでの量子ゲート数とは、1量子ビットまたは2量子ビットに作用する量子ゲート数のことである。 - 15.ハイゼンベルク模型やハバード模型
それぞれ、固体中に局在した相互作用するスピンや、固体中を相互作用しながら動き回る電子の模型。 - 16.ノイズあり中規模量子(NISQ)コンピュータ
誤り訂正機能のない量子コンピュータ。NISQコンピュータでは、量子ビットが環境との相互作用のためにその量子状態(の量子性)を失う前に、計算を完了する必要がある。NISQはnoisy intermediate-scale quantumの略。 - 17.変分量子固有値解法(VQE)
量子コンピュータを用いて量子多体系の基底状態エネルギーなどを計算する変分計算手法。変分パラメータを与えた量子状態(つまり量子回路)によるハミルトニアンの期待値を量子コンピュータで測定し、変分パラメータの更新は通常のコンピュータで行う。VQEはvariational quantum eigensolverの略。 - 18.量子回路の構成に任意性が少ない
量子べき乗法で用いる量子回路は、初期状態を準備する部分と、時間発展演算子を作用させる部分に大別できる。このうち時間発展演算子を作用させる部分の量子回路は、与えられたハミルトニアンに対して系統的に構成できる、という意味で任意性が少ない。初期状態を準備する部分の量子回路の構成には任意性があり、例えばVQEで最適化した量子状態を初期状態として用いるように量子回路を構成してもよい。
研究支援
本研究は、理研HOKUSAIスーパーコンピュータ利用研究課題「Development and application of large scale parallel computing for numerical simulation of strongly correlated quantum many-body systems」、日本学術振興会(JSPS)科学研究費助成事業研究活動スタート支援「ドープされたモット絶縁体における擬ギャップ現象の研究(研究代表者:関 和弘)」、同基盤研究B「対称性が自発的に破れた二次元反強磁性体のマグノン励起とスピノン励起の数値解析(研究代表者:柚木清司)」による支援を受けて行われました。
原論文情報
- Kazuhiro Seki, Seiji Yunoki, "Quantum Power Method by a Superposition of Time-Evolved States", PRX Quantum, 10.1103/PRXQuantum.2.010333
発表者
理化学研究所
創発物性科学研究センター 計算量子物性研究チーム
研究員 関 和弘(せきかずひろ)
チームリーダー 柚木清司(ゆのきせいじ)
(計算科学研究センター 量子系物質科学研究チーム チームリーダー、開拓研究本部 柚木計算物性物理研究室 主任研究員)
報道担当
理化学研究所 広報室 報道担当
お問い合わせフォーム
