理化学研究所(理研)仁科加速器科学研究センター 核構造研究部の大塚 孝治 客員主管研究員(東京大学名誉教授)、東京大学 大学院理学系研究科附属原子核科学研究センターの角田 佑介 特任研究員、筑波大学 計算科学研究センターの清水 則孝 准教授らの共同研究グループは、量子論に基づいて、原子核の形と回転に関する新たな理論体系を提示しました。
この成果は、70年近く信じられてきた原子核の形状と回転の描像とは異なり、教科書の書き換えにもつながるものです。
多くの原子核の形は球形ではなく、楕円体に変形しています。球形から大きく変形した原子核では、断面の一つが円形であるラグビーボール型の軸対称変形[1]が起きるとされてきました。
本研究では、量子論と核力[2]の性質に基づいて原子核の変形の様子を解き明かしました。多くの原子核では三つの主軸の長さが全て異なる楕円体となっており、どの断面も円形にならないアーモンド型の3軸非対称変形[1]が起きていることが理論的に明らかになりました。スーパーコンピュータ「富岳」[3]によるシミュレーションにより、このアーモンド型の描像から得られる結果が既存の実験データと一致しました。原子核の変形について多くの研究者が長く信じてきた見方が大きく転換することになり、それは安定超重元素[4]の探索などにも役立つと期待されます。
本研究は、学術雑誌『European Physical Journal A』(6月2日付:日本時間6月2日)に掲載されました。
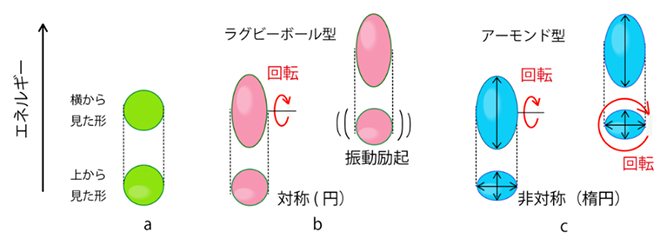
従来のラグビーボール型の原子核(b)と本研究成果のアーモンド型の原子核(c)
背景
原子核は陽子と中性子から成り、その性質や特徴は、陽子数と中性子数によって変わります。原子核の形状は、原子核の内部構造の安定性を示すため、原子核の重要な特徴です。
原子核の形状の研究が始まった当初、原子核の形状は表面張力の働きにより球形となると考えられていました(図1a)。
しかし、1950年代にレインウォーター、ボーア、モッテルソン[5]は、とりわけ重い原子核(陽子数と中性子数の合計である質量数が140以上)が、楕円体であることを見いだし、その結果、1975年にノーベル物理学賞を授与されました。
さらに、ボーアは重い原子核の形状が楕円体の3本の主軸のうち一番長い主軸(図1bの楕円体で上下方向)に対して垂直な断面が円になっているラグビーボール型の軸対称変形となっていることを提唱しました。以来およそ70年間、軸対称変形は、ほとんど全ての重い変形原子核の形状に関する正しい学説とされてきました。その描像は、軸対称変形した楕円体が短軸を軸に回転します(図1b左の赤い円弧矢印)。原子核のスピンが増すとともに楕円体の回転は速くなり、回転運動エネルギーが増加するとされてきました。原子核の円形の断面が波打って振動することも示唆されました(図1b右)。
1950年代にダビドフは図1bとは異なる3軸非対称に変形しているダビドフ模型が多くの原子核で起きていると提案しました。しかし、このダビドフ模型は単純過ぎて実際の実験データを説明することができず、重い原子核の基本的描像として受け入れられませんでした。
1990年代にクラインは、3軸非対称変形を示唆する先駆的な実験データを示しました。しかし、実験データを支える有力な理論がなかったこともあり、多くの研究者には受け入れられませんでした。
このように、現代でも学界では、球形からの大きな変形は極めて多くの重い原子核で起こるが、その形状は軸対称変形に違いないと認識されています。原子核物理学の標準的な国内外の教科書にもそのように記載されています。
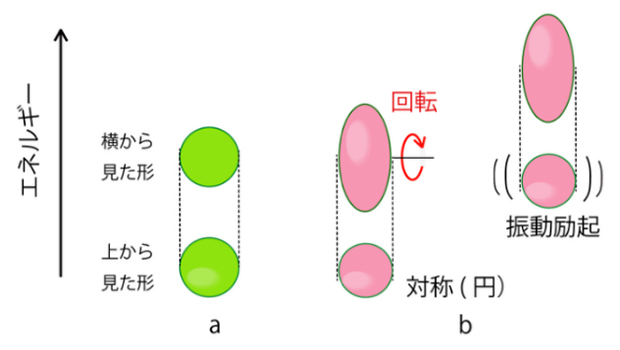
図1 原子核の形・振動・回転の伝統的な描像
(a)球形の原子核。(b)ボーアらが唱えた軸対称変形。楕円体の一番長い主軸に対して垂直な断面が円形。短軸を軸に回転し、円形の断面が波打って振動する。
研究手法と成果
今回、共同研究グループは、球形から大きく楕円体に変形している多くの原子核が、軸対称ではなく、3軸非対称に変形していることを、理論的に示しました(図2b)。
本研究は2本の柱から成ります。1番目の柱は原子核の楕円体への変形や楕円体の量子論的な回転の基本理論の探求、2番目の柱はスーパーコンピュータ「富岳」による原子核構造のシミュレーションです。これらの結果を、原子核のさまざまな状態のエネルギー準位や四重極モーメント、それらの状態の間で起こる電磁励起の強度などの既存の実験データと比較することで、原子核の形状の変形の謎に迫りました。
一例として、ボーアも議論したエルビウム(Er)166という原子核の構造を富岳による計算で明らかにしました。その結果、三つの主軸の長さがどれも異なる楕円体に変形し、3軸の長さの比は0.88、0.93、1.19でした。
この3軸非対称変形の発現と、それによる短軸を軸にした回転(図2b左)と断面に垂直な軸回りの回転(図2b右)の二つの回転の発生が最も重要な理論的発見です。
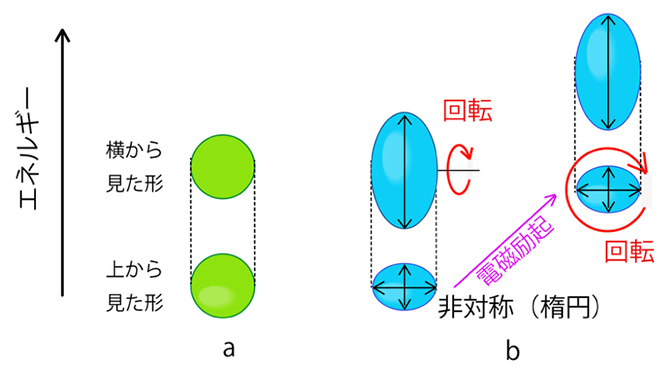
図2 原子核の形・回転の本研究による描像
(a)球形の原子核。(b)本研究成果の3軸非対称変形。楕円体の三つの軸の長さが全て異なっており、どの断面も円形にならない。断面は楕円形で、短軸を軸に回転するだけでなく、断面も回転する。斜め上に上がっていくピンク色の直線矢印は後者の回転を引き起こす電磁励起を表す。
原子核の形状が3軸非対称に変形する二つのメカニズムを見いだし、それを富岳によるシミュレーションで実証しました。3軸非対称性により失われた回転対称性の量子論的回復[6]と核力に含まれる特徴的な成分(テンソル力[2]など)の効果とにより、3軸非対称変形が起きると、軸対称な場合よりも結合エネルギーが増すことを理論的に示しました。
今回発見したこれらメカニズムは、基本的で普遍的なため、多くの原子核で3軸非対称変形が起こっていると予想でき、シミュレーションにより裏付けとなる観測可能な性質を得られました。その一つが図2bの右側の回転を引き起こす電磁励起です。図3で示すように、この電磁励起が起こる強度と3軸非対称変形の大きさ(3軸非対称パラメータガンマ)が、多くの原子核に対してきれいに相関し、また、実験値と理論値もよく一致しています。この相関のような系統的性質も本研究で明らかになりました。
軸対称変形か3軸非対称変形か、という違いは取るに足りないことと思われるかもしれません。しかし、3軸非対称変形は、エネルギー準位のパターンや図3で示されている電磁励起強度など原子核の多様な性質に関わり、種々の実験データにも反映される重要な性質です。
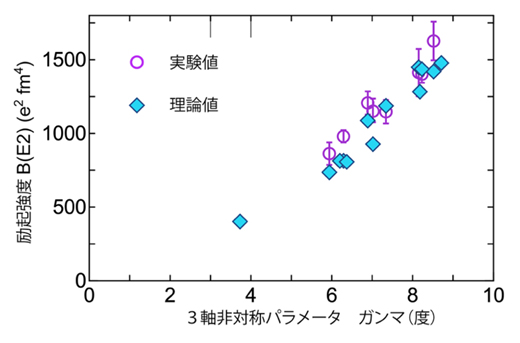
図3 電磁励起強度による3軸非対称変形の検証
さまざまな原子核の電磁励起の強度の理論計算値(青の菱形)や既存の実験データ値(紫の丸)を表示。横軸は3軸非対称パラメータであるガンマであり、3軸非対称変形の大きさを角度(度数)で表し、0のときは軸対称、大きくなるほど非軸対称性が増す。理論値と計算値ともに、多くの原子核に対してガンマとよく相関し、また、理論値と実験値はよく一致している。
縦軸に陽子数、横軸に中性子数をとって既知および概念上の核種を配置した核図表において、原子核の形状が分かるように表現しました(図4)。エネルギー準位の既存実験データによって球形から大きく変形した楕円体であることが分かっていた核種(丸、菱形、六角形)と、富岳によるシミュレーションで強めの3軸非対称変形が起きていることが確認された核種(オレンジの丸)と、球体や球体から小さく変形した楕円体の核種(四角い升目)とを表示しました(図4)。
3軸非対称変形であることが今回確認された核種(オレンジの丸)は、ボーアやその後いくつかの研究でも軸対称変形とされてきたことを考えると、今回の成果は原子核の描像における大きな転換点となります。
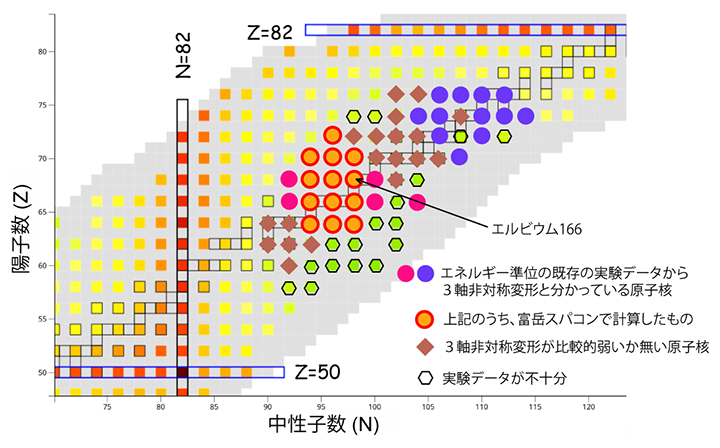
図4 核図表に表示した3軸非対称変形をした原子核
核図表の一部(陽子数Z=50~82、中性子数N=82~122)。3軸非対称変形した原子核を丸(富岳で計算したものはオレンジ)で、それ以外を菱形で示した。変形楕円体だが実験データの不足で3軸非対称変形か判定不能のものは六角形で表す。それら以外の四角い升目は、変形が小さいか球体を示す。
本研究では、3軸非対称変形の広範な出現に加えて、量子論における回転運動がどういうものであるかを明確に述べました。既に触れたように、ボーアの模型では、楕円体に変形した原子核はあたかも自由に回転する剛体のように扱われ、剛体の自由な回転運動エネルギーを量子論で扱った式で実験データを説明できる、というものでした。
しかし、原子核のようなミクロな多体系を量子論で考えると、違った描像が現れます。原子核の形が楕円体のように変形すると、それは空間のいろいろな方向を向くことができます。量子論ではいろいろな方向の楕円体状態を重ね合わせてさまざまなスピンを持った量子状態をつくります。このような飛び飛びのスピンを持った量子状態が回転バンド(帯)を構成します。この回転バンド内のエネルギー準位がスピンとともに増加するメカニズムが明らかになりました。つまり、スピンが増すとともにエネルギー準位が上がっていく性質は、旧来説の回転による運動エネルギーの増大ではなく、結合エネルギーの変化であることを明確に示しました。これが、原子核のような多数の粒子から成るミクロなシステムの「回転」の量子論による描像ですが、これまでほとんど認識されていませんでした。さらに、そのような回転の「慣性モーメント」に相当する量の計算式なども得られ、量子論的な全体像が定性的にも、定量的にも示されました。
このように、量子論と古典論をつなぎ合わせて1950年代にできた原子核回転状態の記述を、本研究では、3軸非対称変形も含め、量子論だけで書き換えることに成功しました。結果的には既存の実験データを核力から出発して説明し、未知の新たな回転バンドも予言しました。原子核の回転バンドの包括的な記述が量子多体論のレベルで可能になり、ユネスコの「国際量子科学技術年(2025年)」にふさわしい成果といえるかもしれません。
今後の期待
本研究の成果により、原子核の形状が3軸非対称変形となることで、軸対称な場合よりも結合エネルギーが大きくなり安定化することが明らかになりました。これは、原子核の基本的で普遍的な性質であるため、安定または準安定な超重元素原子核の理論からの探索や、重い原子核の構造解明に大いに役立ちます。
まず超重元素[4]の原子核では変形による結合エネルギーが、より軽い原子核に比べてさらに重要になると考えられます。
また、従来の理論では取り組む手法がよく分かっていなかった重い原子核(質量数が100を十分に超えるもの)の構造解明に、今回の理論を使うことができると想定できます。今後、理研のRIビームファクトリー(RIBF)[7]や欧州原子核研究機構のLHC[8]など、さまざまな施設での実験で今回の理論の正当性が検証されると期待されます。
今回の研究では、原子核の陽子数も中性子数も偶数の場合を扱いましたが、それらのどちらかが奇数の原子核(奇核)にも本研究の知見を拡張できると考えています。例えば、トリウム229[9]の基底状態と励起状態の間の電磁遷移の寿命は原子核時計に適しており、本研究の成果に基づいて、それらの量子状態の多体構造を調べ、形や配位、さらにはその遷移が電気的か磁気的か、などを明らかにすることで、究極精度の原子核時計となるかもしれません。
近年、RHIC[8]やLHCで、相対論的重イオン衝突により、10のマイナス25乗秒程度の時間スケールで原子核の構造を見ようとする試みが始まっています。本研究の対象の3軸非対称変形は既にこれらの加速器の実験計画の検討課題に含まれており、実際、国際共同研究が始まっています。
今回の研究では回転を扱いましたが、その対極として振動があり、今後は回転と振動を統一する研究を進めたいと考えています。
補足説明
- 1.軸対称変形、3軸非対称変形
原子核の形状は球体や楕円体である。楕円体には主軸が3本あり、その中の最も長い主軸以外に、残りの2本の主軸の長さが等しい場合に軸対称と呼ばれる。一方、残りの2本の長さが異なると3軸非対称と呼ぶ。軸対称な楕円体変形では、円形の断面に垂直な軸の長さが円の直径よりも長いが、短い場合もあり得る。軸対称変形をプロレート変形、3軸非対称変形をオブレート変形と呼ぶ。実際の原子核ではプロレート変形が圧倒的に多く、本研究でもプロレート変形を暗黙の前提として想定している。 - 2.核力、テンソル力
陽子と中性子を総称して核子と呼び、核子の間に働く力を核力という。電磁気力や重力ではなく、強い相互作用の分類に属する。核力には中心力成分に加えて、重要な成分としてテンソル力がある。それは2個の核子のスピンや相対位置が独特の結合をしているときにのみ働き、核力を特徴付ける性質の一つである。 - 3.スーパーコンピュータ「富岳」
スーパーコンピュータ「京」の後継機。2010年代に、社会的・科学的課題を解決することで日本の成長に貢献し、世界をリードする成果を生み出すことを目的とし開発が始まった。電力性能、計算性能、ユーザーの利便性・使い勝手の良さ、画期的な成果創出、ビッグデータやAIの加速機能の総合力において世界最高レベルのスーパーコンピュータとして2021年3月に共用を開始した。現在「富岳」は日本が目指すSociety 5.0を実現するために不可欠なHPCインフラとして活用されている。 - 4.安定超重元素、超重元素
超重元素は原子番号104のラザホージウム(Rf)以降の元素を指す。原子番号114のフレロビウム(Fl)の中性子数184付近の同位体に安定な(あるいは準安定な)超重元素があるのではないかと考えられ、探索の努力が続けられている。理研が発見した原子番号が113のニホニウム(Nh)も超重元素の一つである。 - 5.レインウォーター、ボーア、モッテルソン
原子核の変形の研究を創始した物理学者で氏名は順に、Leo J. Rainwater、Aage Bohr、Ben R. Mottelson である。オーゲ・ボーアはNiels Bohr(ニールス・ボーア)の子である。3氏は1950年代に出版された論文で、1975年にノーベル物理学賞を受賞した。本研究に最も関わるのはボーアの理論である。 - 6.回転対称性の量子論的回復
原子核は一般に真空中にあり、どの方向も対等、つまり対称である。一方、表面の形が球体から楕円体に変形すると、この対称性が壊される。壊された対称性は回復される必要があり、量子状態の持つスピンに応じたパターンで、方向に応じて値が変わる重みで、いろいろな方向を向いた楕円体状態が重ね合わされる。これを回転対称性の回復と呼び、量子論の基本的な性質である。 - 7.RIビームファクトリー(RIBF)
水素からウランまでの全元素のRI(不安定原子核)を世界最大強度でビームとして発生させ、それを多角的に解析・利用することにより、基礎から応用にわたる幅広い研究と産業技術の飛躍的発展に貢献することを目的とする最先端加速器施設。施設はRIビームを生成するために必要な加速器系、RIビーム分離生成装置(BigRIPS)で構成されるRIビーム発生系施設、および生成されたRIビームの多角的な解析・利用を行う基幹実験装置群で構成される。これまで生成不可能だったRIも含めて約4,000種類のRIを生成できると期待されている。 - 8.LHC、RHIC
LHCは欧州原子核研究機構(CERN)に設置されている大型ハドロン衝突型加速器、RHICは米国ブルックヘブン国立研究所(BNL)に設置されている相対論的重イオン衝突型加速器。いずれも相対論的な高エネルギーまで原子核を加速できる。当初はクォーク・グルーオン・プラズマなどの研究に使われてきたが、最近は原子核の形状の測定にも使われている。 - 9.トリウム229
原子番号90(元素記号はTh)のアイソトープで中性子数139のもの。基底状態のスピン・パリティが5/2+で、8.4電子ボルトという極めて低い励起エネルギーに、暫定的なスピン・パリティが3/2+の状態があり、この2状態間の電磁遷移を究極の精度の原子核時計として使う先端的な研究が世界各地で行われている。これらの状態の量子多体構造を明らかにするのは本研究の延長線上にあるが、他の理論手法では難しい。
共同研究グループ
理化学研究所 仁科加速器科学研究センター 核構造研究部
客員主管研究員 大塚 孝治(オオツカ・タカハル)
(東京大学名誉教授)
部長 上野 秀樹(ウエノ・ヒデキ)
東京大学 大学院理学系研究科附属原子核科学研究センター
特任研究員 角田 佑介(ツノダ・ユウスケ)
筑波大学 計算科学研究センター
准教授 清水 則孝(シミズ・ノリタカ)
日本原子力研究開発機構先端基礎研究センター
研究主席 宇都野 穣(ウツノ・ユタカ)
慶應義塾大学 理工学研究科
特任准教授 阿部 喬(アベ・タカシ)
研究支援
本研究は、文部科学省ポスト「京」重点課題9「宇宙の基本法則と進化の解明」、同「富岳」成果創出加速プログラム「シミュレーションでせまる基礎科学:量子新時代へのアプローチ(PMXP1020230411)」「シミュレーションで探る基礎科学:素粒子の基本法則から元素の生成まで(JPMXP1020200105)」および計算基礎科学連携拠点(JICFuS)の元で実施したものです。また、本研究の一部は、スーパーコンピュータ「富岳」の計算資源の提供を受け、実施しました(課題番号:hp200130、hp210165、hp220174、hp230207、hp240213)。
原論文情報
- T. Otsuka, Y. Tsunoda, N. Shimizu, Y. Utsuno, T. Abe, and H. Ueno, "Prevailing Triaxial Shapes in Atomic Nuclei and a Quantum Theory of Rotation of Composite Objects", European Physical Journal A, 10.1140/epja/s10050-025-01553-1
発表者
理化学研究所
仁科加速器科学研究センター 核構造研究部
客員主管研究員 大塚 孝治(オオツカ・タカハル)
(東京大学名誉教授)
東京大学 大学院理学系研究科附属原子核科学研究センター
特任研究員 角田 佑介(ツノダ・ユウスケ)
筑波大学 計算科学研究センター
准教授 清水 則孝(シミズ・ノリタカ)
発表者のコメント
科学者は、今信じていることに本当はどこまで根拠があるのか、今手にしているものが本当に真実なのかを、時々見直す心構えや懐の深さも必要なのではと思う次第です。(大塚 孝治)
 大塚 孝治
大塚 孝治
報道担当
理化学研究所 広報部 報道担当
お問い合わせフォーム
東京大学大学院理学系研究科 理学部 広報室
Tel: 03-5841-8856、Email: media.s@gs.mail.u-tokyo.ac.jp
筑波大学 計算科学研究センター 広報・戦略室
Tel: 029-853-6260、Email: pr@ccs.tsukuba.ac.jp
