自然界には、多種多様な生物が複雑に関わり合いながら進化し形づくってきたさまざまな生態系が存在します。その構造の複雑さゆえに仕組みを理解するのは至難の業。数理モデルを使って生態系を記述することで、その謎に迫ろうとしている研究者が理研にいます。数理創造プログラム(iTHEMS)の入谷 亮介 上級研究員に話を聞きました。
生物多様性の謎が主要な研究テーマに
生物多様性。それは多種多様な生物がつながり合いながら存在していることを示す言葉だ。入谷 上級研究員は、数理モデルの研究を通して870万種ともいわれる生物の多様性、特に生態系に関するさまざまな謎の解明を目指している。数理モデルとは自然現象や社会現象など、時間の経過とともに変化する複雑な世界を、数学の式を使って理解しようとするものだ。
「既存の研究では、複雑な相互作用のなかで多様な生物が共存している背景に潜む普遍的法則が、見いだされてはいませんでした。多様性と普遍性の関係を解き明かすことで、生態系の在り方を理解してみたいと思うようになりました」
例えば、1859年にチャールズ・ダーウィンは著書『種の起源』の中で、自然選択説を提唱した。突然変異によって生まれた、生存競争上の優位性の高い遺伝子のみが、後世に引き継がれるという理論だ。自然界では生物は日々熾烈な生存競争にさらされており、捕食者と被食者、競合関係、環境要因やそれに対する適応の度合いの差に伴い、生物の個体数は時間の経過とともに常に変化している。
確かに、自然界がいわゆる「弱肉強食」の世界なのであれば、「弱者」は淘汰され尽くし、多様な世界は実現しそうにない。しかし実際には、多種多様な生物が共存している。これは世界中のあらゆる地域で共通な経験則だ。ということは、生態系が多様化するプロセスの中にも、共通法則があるのかもしれない。
そこで入谷 上級研究員は、所属するiTHEMSの研究員たちと共に、生物多様性の法則を説明する上で既存の進化・生態系の数理モデルに共通する要素を発見すべく、数理モデルの再構築・解析に取り組んだ。そして、統計物理学で用いられる確率的な数理モデルを応用し、生物の個体数頻度の変化の様子を数理モデル化したところ、生物集団の個体数の変化を記述できる一般的な式(「速度限界不等式」)があることを発見したのだ。
その不等式からは、複数種類の生物種から成る生態系において、個体群を特徴づける、例えば増殖率を含むあらゆる量の変化速度は、ある共通の値よりは決して大きくなり得ないことが分かった(図1)。また、この式は個体群の自然選択だけでなく、遺伝子の突然変異を伴う進化においても成り立つことが確かめられた。「まだまだ生物多様性の謎の解明には至っていませんが、その時間変化の共通法則の存在を解明でき、大きな手がかりをつかんだと考えています」
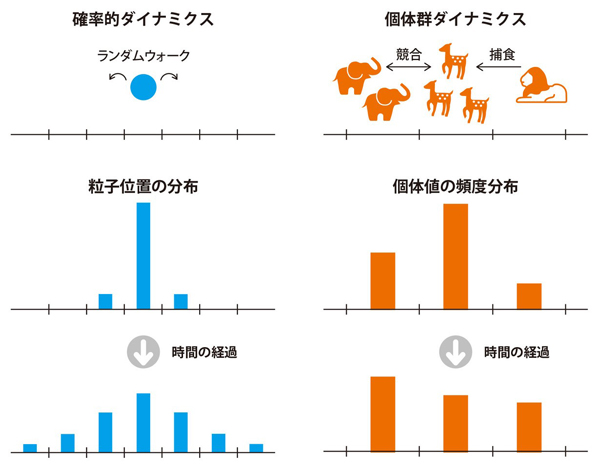
図1 確率的ダイナミクスと個体群ダイナミクスの類似性
得られた速度限界不等式は、生態系の多様度(さまざまな生物種が共存しているとき、種の多様性の度合いを表す指標)の評価にも適用できることが分かった。つまり、多様な種の共存の背景にも、共通の法則が存在しているのである。これにより、進化や生態系における複雑な個体群、そして、それを構成する個体数の時間的な変化を統一的に理解できるようになることが期待される。
重要なのはシンプルさと複雑さのバランス
そもそも生態系の謎の解明に、数理モデルを使うメリットはどこにあるのだろう。「生態系は本当に複雑。現象が複雑であればあるほど、その現象の背景にある根本的な部分や共通部分を見つけ出すことが重要です。数理モデルを使ってそれを表現することで、複雑な現象を理論的に説明できるようになるのです。"数理生物学"と呼ばれるこのアプローチは近年、盛んに行われていますが、中でも私は生態系に着目しており、これは"数理生態学"と呼ばれています」
植物や動物など、地球上のあらゆる生物は、それぞれ異なる生存戦略をとりながらも、その背景には「自分の遺伝子を残す」という共通の目的がある。その視点から生物を眺めると、一見異なるように見える行動を、一つの理論で説明できるようになるという。「たとえば、タンポポは綿毛を飛ばすことで種子を遠くに運ぶ戦略をとっています。自分の遺伝子を広く移動、分散させればそれだけ危険や脅威にも遭遇しますが、同じ親から生まれた血縁者同士で争うことを回避しているのです。血縁者同士の相互作用が重要であるというのは、アリやハチのような卓越した社会性を持つ動物についても同様です」
生物に共通する理論を抽出し数理モデルを構築する上で、入谷 上級研究員が最も意識している点が、「シンプルさと複雑さのバランスをとること」だ。よりシンプルな数理モデルの構築は、その数理モデルに汎用性を持たせることができる反面、個々の事例を正確に表すことができなくなる。しかし、個々の事例をより正確に表すためにパラメータの数を増やすと、汎用性が失われるだけでなく本質も見えづらくなる。そのため、絶妙なバランスを探ることが、数理モデルに求められる重要な課題なのだ。
幅広い分野の研究者との議論で刺激的な毎日
現在の研究を始めたきっかけは、大学生時代に遡る。京都大学理学部に進学したものの、子どもの頃から大好きだった数学と生物の二つの分野は、乖離しているように思われた。どちらの道を選ぶか悩んでいたところ、図書館で『数理生物学入門』という本を偶然見つけ、数理生物学の存在を知った。この分野であれば、数学と生物学の両方を研究したいという自分の夢を実現できる。そこで、数理生物学を志し、この本の著者である巌佐 庸 教授(当時)のいる九州大学大学院のシステム生命科学府に進学した。
その後、フランスやスイス、イギリス、アメリカの大学で研究員を務め、2019年にiTHEMSの研究員として採用され、理研にやってきた。「iTHEMSの良いところは、生物学、数学、物理学をはじめ、さまざまな分野の研究者とフラットな立場で自由に議論できること。独創的な研究が次々と生まれる環境で、ほかでは経験できない刺激的な毎日を送っています」
目標は、自分の研究を生物多様性の保全や環境保護につなげることだ。「そのためには、数理モデルを使って未解決問題を解明し、適切な対策を打つことが重要です。今後も幅広い分野の研究者たちと共同研究を続けながら、目標に向かって歩んでいきます」と決意を新たにする。
(取材・構成:山田 久美/撮影:相澤 正。/制作協力:サイテック・コミュニケーションズ)
関連リンク
- 2022年6月1日プレスリリース「進化・生態ダイナミクスの共通法則-生物の個体群変化を物理学的な関係式で記述する-」
この記事の評価を5段階でご回答ください

