要旨
理化学研究所(理研)脳科学総合研究センター神経適応理論研究チームの豊泉太郎チームリーダーらの研究チーム※は、神経回路型ハードウェア用いて複数の感覚入力を独立した成分に分解するためのアルゴリズム[1]を開発しました。
騒がしいパーティー会場で、複数の話者の話し声の中から注目する人の声を聞き分けることができるように、脳は複数の感覚入力を独立した成分に分解して処理することができます。この処理を「独立成分分析(ICA)[2]」と呼びます。これまで、計算機上でICAを実現するためのアルゴリズムが提案されていますが、神経ネットワークを模倣した神経回路型ハードウェア[3]への実装はさまざまな制限があり困難でした。
研究チームは、複数の信号源が混在する感覚入力を表現する入力神経細胞と感覚入力の中から元となる信号源の成分(独立成分)を抽出する出力神経細胞との間のシナプス強度[4]を、経験に応じてどのように変化させたらICAを実現できるかを調べました。その結果、シナプス強度の変化を「広域信号×入力神経細胞の活動×出力神経細胞の活動」で表現する新しい計算方法を発見し、「error-gated Hebbian rule(EGHR)」と名付けました。広域信号は、それぞれの出力神経細胞の活動度に依存した信号を単純に足し合わせることで計算され、各シナプス結合で起こる「ヘッブ型可塑性[5]」の速さと方向を一元的に調節する仕組みになっています。
続いて、数理解析と計算機シミュレーションによってEGHRと従来法を比較しました。すると、従来法が出力神経細胞の数と信号源の数が等しくないと働かないのに対し、EGHRは神経細胞の数が信号源の数より多ければICAを実現できることが分かりました。すなわち、EGHRでは、神経細胞の数が充分沢山あれば信号源の数が動的に変化する現実的環境でも柔軟にICAを実現できることが分かりました。そして、EGHRは自然画像や動画に対して、ICAを容易に実現しました。
今後、神経回路型ハードウェアを用いた並列計算[6]による、高速に画像・音声信号の要素分解が可能になると期待できます。また、EGHRは、神経ネットワーク内の多数の神経細胞が協調的に動作することで感覚入力の背後にある隠れた原因を読み取る過程をうまく説明できるため、これまで詳細が分からなかった生命科学・工学・医学の境界領域を開拓できる可能性があります。
本研究は、英国のオンライン科学雑誌『Scientific Reports』(6月21日付け:日本時間6月21日)に掲載されました。
※研究チーム
理化学研究所 脳科学研究センター 神経適応理論研究チーム
チームリーダー 豊泉 太郎(とよいずみ たろう)
研修生 磯村 拓哉(いそむら たくや)
背景
騒がしい場所で、複数の話者の話し声の中から特定の話者の声を聞き分けられることを「カクテルパーティ効果」と呼びます。このように脳には、複数の信号源が混在する感覚入力をうまく分解し、独立した情報として処理する能力があります。この能力を計算機上で再現するために、さまざまなアルゴリズムが提案されています。「独立成分分析(ICA)」もその一つです。
脳の神経細胞は、互いに電気信号をやり取りすることで複雑な情報処理をしています。私たちが経験を通じて学習できるのは、脳内の神経細胞間のシナプス強度が動的に変化する「可塑性」という性質を持つためです。これまでの研究から、神経細胞間で頻繁に使われたシナプス結合はより強くなり、あまり使われなかったシナプス結合はより弱くなるという「ヘッブ型可塑性(Hebbian plasticity)」によって、学習が進むと考えられています。
研究チームは、今回、感覚情報を表現する入力神経細胞と独立成分を抽出する出力神経細胞の間のシナプス強度(図1上)を、経験に応じてどのように変化させたらICAを実現できるかを調べ、神経回路型ハードウェアにICAを実装可能とする新しいアルゴリズムの開発に取り組みました。
研究手法と成果
脳の神経回路網を模倣した神経回路型ハードウェアでICAを行うには、その計算方法は各神経細胞が並列・分散的に情報処理をするのに適したものである必要があります。
研究チームはまず、神経回路の数理モデルを作成しました。現在、工学的によく用いられている計算方法では、神経細胞間に密な情報共有を必要としており、神経回路型ハードウェアに実装することは困難です。これまで、神経回路型ハードウェアへ実装可能な計算方法も提案されていますが、研究チームの解析の結果、これらの従来法は信号源の分解の失敗につながる条件を多く持っており、適用範囲が狭いことが明らかになりました。さらに従来法では、実際に神経細胞間で観測されるよりも密度の高い配線が必要であることが分かりました。そのため従来法では、計算量とコストの両面の制約から、神経回路型ハードウェアで大規模なICA計算を実現することができませんでした。
一方、近年の生理実験により、ヘッブ型可塑性は入出力の神経細胞の活動だけでなく、より広域に伝わる「分子信号(広域信号)」の影響も受けることが分かってきました。そこで研究チームは、従来法では出力神経細胞間のシナプスが担っていた相互作用を、広域信号によるヘッブ型可塑性の調節で代替することで、神経細胞間の密度の高い配線を不要とすることを目指しました。
本研究で開発した新しい計算方法では、シナプス強度の変化を「広域信号×入力神経細胞の活動×出力神経細胞の活動」という形で表現しています。広域信号は、それぞれの出力神経細胞の活動度に依存した信号を単純に足し合わせることで計算され、各シナプス結合で起こるヘッブ型可塑性の速さと方向を一元的に調節する仕組みになっています(図1下)。研究チームは、広域信号に偏差(エラー)の意味があることから、新しい計算方法を「error-gated Hebbian rule(EGHR)」と名付けました。
続いて、数理解析と計算機シミュレーションによって、EGHRと従来法を比較しました。そして、EGHRが従来法よりも計算の並列化に優れていること、従来法が処理できなかった時間的変動の速い信号にも対応でき適用の範囲が広がること、従来法ではうまく働かないさまざまな状況下でもICAを実行できることを示しました。特に、従来法が出力神経細胞の数と信号源の数が等しくないと働かないのに対し、EGHRは十分に多い神経細胞があれば、信号源の数が少ない場合でも、ICAを実行できることが分かりました。すなわち、EGHRでは、信号源の数が動的に変化する現実的環境でも柔軟に計算できることが明らかになりました。更に、EGHRは自然画像(図1上)や動画(図2)に対しても、ICAを容易に実現しました。
今後の期待
本成果で開発したEGHRは、近年開発が進む神経回路型ハードウェアと組み合わせることで、サンプルデータではない“現実のデータ”の大規模な並列処理を可能にします。高速な画像・音声信号の要素分解の実現など、工学や生命科学などさまざまな分野にインパクトを与えると期待できます。
また、EGHRを用いると、神経ネットワーク内の多数の神経細胞が協調的に動作することで、感覚入力の背後にある隠れた原因を読み取る過程をうまく説明できます。そのため、これまで詳細が分からなかった生命科学・工学・医学の境界領域を開拓できる可能性があります。
原論文情報
- Takuya Isomura, Taro Toyoizumi, "A Local Learning Rule for Independent Component Analysis", Scientific Reports, doi: 10.1038/srep28073
発表者
理化学研究所
脳科学総合研究センター 神経適応理論研究チーム
チームリーダー 豊泉 太郎(とよいずみ たろう)
報道担当
理化学研究所 広報室 報道担当Tel: 048-467-9272 / Fax: 048-462-4715
補足説明
- 1.アルゴリズム
コンピュータを動かして特定の目的を達成させるために必要な情報処理の方法や手順のこと。ここでは学習則のこと。 - 2.独立成分分析(ICA)
混ざり合った複数の入力から、その背後にある個々の信号源を取り出すための工学的手法の一種。この分析手法は、例えば、複数マイクで観測した音声信号の重ね合わせを元の独立な信号に分離するという課題で、潜水艦のソナー解析、ビデオ動画使った生体信号検出など、さまざまな分野で応用されている。ICAは、Independent component analysisの略。 - 3.神経回路型ハードウェア
神経細胞を模倣した計算素子が互いに結合したネットワークからなる計算装置のこと。 - 4.シナプス強度
シナプスは神経回路において、一つの神経細胞と次の神経細胞がつながる部分。神経細胞の末端に存在するわずかな隙間で、ここを介して情報がやりとりされている。シナプスにおける情報伝達率をシナプス強度と呼ぶ。化学シナプスの場合は、シナプスにおける神経伝達物質の放出量や受容体の量などによって、情報伝達率が変化する。 - 5.ヘッブ型可塑性(Hebbian plasticity)
神経細胞同士をつなげるシナプスにおいて、シナプス前の神経細胞の活動の直後にシナプス後の神経細胞の活動が起きることが繰り返されると、そのシナプス結合は増強され、逆にそのような活動が長時間起きないと、そのシナプス結合は減弱するという現象。カナダの心理学者ドナルド・ヘッブが提唱した。 - 6.並列計算
複数の計算素子を使って一つの問題を解くこと。
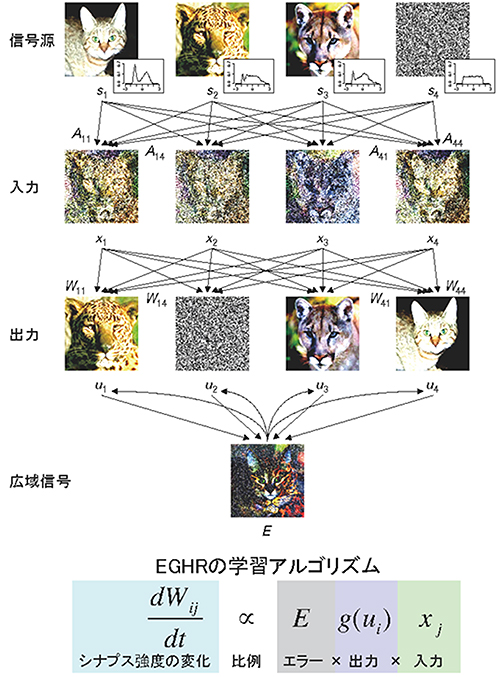
図1 神経回路モデルの構造と学習アルゴリズム
上部:数理モデルは、信号源si(1段目)、感覚入力(入力)xi = ∑j Aij sj(2段目)、出力神経細胞の活動(出力)ui = ∑j Wij xj(3段目)、広域信号 E = ∑i f(ui)(4段目)からなる。ここで、iやjは複数ある信号源や神経細胞を特定するための添字、Aij は信号源がどのように環境中で混じり合っているかを表現する係数、Wij はシナプスの強さを表す係数、fは非線形関数である。出力神経細胞の情報表現が特定の信号源に偏るのを避けるため、広域信号によって入出力細胞間のシナプス可塑性を調節した。
下部:学習アルゴリズムの数式。EGHRに従いシナプス強度Wijを学習させると、出力神経細胞がそれぞれ独立な信号源を表現するように学習し、背後の信号源を推定できることを示した。数式中のdWij/dtはシナプス強度の時間変化、gは非線形関数。
Isomura, Toyoizumi, Sci Rep, 2016より改変。画像はCaltech101 dataset(Fei-Fei et al.,IEEE CVPR ,2004, 2003)より。

図2 EGHRによる自然動画の独立成分への分解
EGHRによる自然動画のICA。信号源として4つの動画を用意し(上段)、それらを混ぜ合わせて入力を生成(中段)。EGHRは自然動画に対してもICAを実行可能であり、出力(下段)は元の動画(信号源)をうまく復元することができた。
Isomura, Toyoizumi, Sci Rep, 2016より転載。動画は
MotionElements(英語)より。
