理化学研究所(理研)数理創造プログラムの儀保伸吾特別研究員と黒澤元研究員の研究チームは、「体内時計[1]」が温度によらず約24時間周期で時を刻むメカニズムには、生体分子の振動波形のひずみが重要であることを発見しました。
本研究の成果は、これまでの体内時計の研究にはない新しい着眼点です。今後、生体分子の時系列波形についての高精度な測定による実験検証が行なわれれば、波形の解析による体内時計の詳細なメカニズムの解明につながると期待できます。
地球上の多くの生物は、地球環境の1日の変化に適応するために、約24時間周期の体内時計を持っています。生物の体内時計は、化学反応のネットワークによって構成されています。一般に、温度が高くなるほど化学反応は速く進みますが、体内時計の周期は温度によらず約24時間でほとんど変わりません。この性質は、「体内時計の温度補償性」と呼ばれています。
今回、研究チームは、体内時計の数理モデル[2]を解析し、化学反応の速さと体内時計の周期との関係式を導き出しました。その結果、温度が高くなっても周期が安定であるためには、温度が高くなるとともに生体分子の振動波形がサイン波よりひずむことが必要であるということが分かりました。
本研究は、米国の科学雑誌『Biophysical Journal』への掲載に先立ち、オンライン版(1月15日付け)に掲載されました。
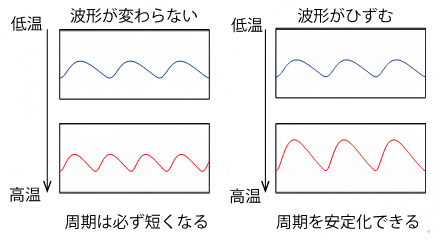
図 高温で波形がひずむことによる周期の安定化
※研究支援
本研究は、科学技術振興機構(JST)戦略的創造研究推進事業(CREST)の研究領域「生命動態の理解と制御のための基盤技術の創出(研究総括:山本雅)」研究課題名「クロノメタボリズム:時間相の生物学(研究代表:岡村均)」による支援を受けて行われました。
背景
生命現象の中には、体内時計、細胞分裂の周期、体節時計[3]など、周期的に振動する現象がいくつかあります。これらの現象は、生体内の遺伝子発現や化学反応のネットワークによって構成されています。一般に、温度が高くなるほど、化学反応は速く進むため、多くの生物振動現象の周期は短くなります。しかし、体内時計の周期は、温度によらず約24時間でほとんど変化しないことが知られています。この現象は、「体内時計の温度補償性」と呼ばれていますが、その仕組みはよく分かっていません。
長年の研究の間に、温度補償性を説明するための仮説がいくつか提案されてきました。例えば、温度を高くすると、周期を長くする反応と短くする反応が同じ程度活性化され、全体の周期を維持するという仮説(バランス仮説)や、周期を大きく変える反応の進み方は温度によって変わらないため、周期はほとんど変化しないという仮説(クリティカル反応仮説)、温度が高くなることによる反応の速さの上昇とともに振幅も大きくなることで、周期が一定に保たれるという仮説(振幅仮説)があります。
こうした仮説を検証し、温度補償性のメカニズムを解明するにあたっては、体内時計を構成する生体分子のさまざまな振動波形が新たな手がかりとなる可能性があります。
研究手法と成果
研究チームはまず、振動波形の違いに着目し、振動波形のひずみの大きさを、サイン波からのズレの大きさとして定量化できる指標を導入しました。サイン波とは、三角関数という単純な数式で表現される最も基本的な波のことです。サイン波からのひずみの指標は、波形を周波数解析したときの「高い周波数成分の大きさ」として計測できます(図1)。
次に、哺乳類やショウジョウバエなどの体内時計の制御ネットワークを模した数理モデルを構築し、その周期を数学的に導出しました。その結果、体内時計の周期は、化学反応の速さに反比例し、波形のひずみの大きさに比例することが分かりました。
この解析結果から、温度補償性に関して二つのことが予想できます。一つは、温度にかかわらず生体分子の振動波形が変わらなければ、温度が高くなって化学反応の速さが上昇したとき、必ず周期は短くなるということです。もう一つの予想は、温度が高くなっても周期が変化しない場合、波形は必ずサイン波よりもひずんでいるということです。これらの予想は、「体内時計の周期が温度補償性をもつためには、高温で波形がサイン波よりひずむ必要がある」と言い換えることができます。
この予想は、前述のバランス仮説、クリティカル反応仮説、振幅仮説のいずれが正しくても成り立ちます。このことから、波形のひずみによる体内時計の周期の安定化は、従来の仮説を統合する新たな仮説といえます。さらに、哺乳類やショウジョウバエと異なるネットワークを持つシアノバクテリアの体内時計[4]の数理モデルや、非線形性の電気回路などで使われるvan der Polモデル[5]でも、同様の結果が得られることも分かり、多くの振動系において普遍的に見られる結果であることが示唆されます(図2)。
今後の期待
体内時計の温度補償性を実現するためには高温で波形がひずむ必要があることを示した本研究は、今後、生体分子の変動のより高精度な測定によって実験検証されることで、体内時計についてのより深い理解につながることが期待できます。
体内時計の数理モデルを含む多くの振動系について、波形のひずみが周期を長くする仕組みはまだよく分かっていません。非線形振動系において波形に着目した研究は少なく、本研究は理論的な観点からも大きく発展していく可能性があります。
原論文情報
- Shingo Gibo, Gen Kurosawa, "Non-sinusoidal Waveform in Temperature-Compensated Circadian Oscillations", Biophysical Journal, 10.1016/j.bpj.2018.12.022
発表者
理化学研究所
数理創造プログラム
特別研究員 儀保 伸吾(ぎぼ しんご)
研究員 黒澤 元(くろさわ げん)
 儀保 伸吾
儀保 伸吾
報道担当
理化学研究所 広報室 報道担当
Tel: 048-467-9272 / Fax: 048-462-4715
お問い合わせフォーム
産業利用に関するお問い合わせ
補足説明
- 1.体内時計
多くの生物が持つ約24時間周期のリズム現象。哺乳類やショウジョウバエの場合は、細胞内のタンパク質が遺伝子発現を調節することで生じる、遺伝子活性の約24時間の周期的な変動である。 - 2.数理モデル
複雑な現象の一面を簡略化した形で表現し、微分方程式など数式を用いて記述したシステムのこと。 - 3.体節時計
脊椎動物の体幹部に見られる繰り返し構造を体節と呼ぶ。発生の過程において、決まった時間周期で組織がくびれることで、体節の繰り返し構造が形成される。体節時計とは、組織がくびれる時間周期を決める機構のこと。 - 4.シアノバクテリアの体内時計
シアノバクテリアとは、光合成をおこなう原核単細胞生物の一種である。シアノバクテリアの体内時計では、遺伝子発現がなくても、三つのタンパク質(KaiA、KaiB、KaiC)とATPによって、タンパク質の化学反応(リン酸化と脱リン酸化)が約24時間の周期で繰り返される。 - 5.van der Polモデル
抵抗による電圧の減衰が電流の大きさに比例しない場合(非線形性)の電気回路など、多くの振動現象の解析に幅広く利用されている振動方程式。
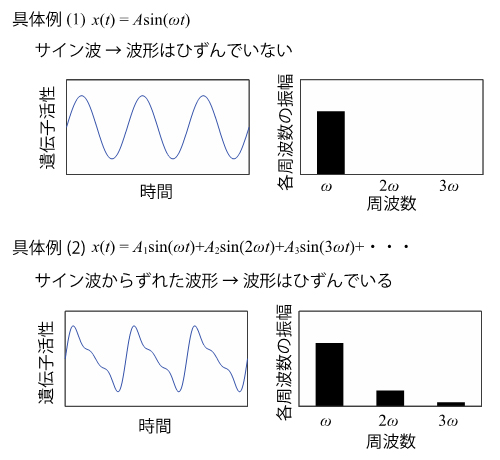
図1 波形のひずみの具体例
一般に、周期的な振動波形は、複数の三角関数の足し算で表すことができる。
- (上) 遺伝子活性の振動波形が一つの三角関数(Asin(ωt))のみで表されるサイン波の場合、波形はひずんでいない。このとき、高い周波数(2ω、3ω、・・・)の振幅は0である。ωは三角関数の周期の単位2π(ラジアン)を振動全体の周期で割ったもの。体内時計におけるωは2πを約1日で割ったもの。
- (下) 遺伝子活性の振動波形がたくさんの三角関数の足し算(A1sin(ωt)+A2sin(2ωt)+A3sin(3ωt)+・・・)で表され、高い周波数(2ω、3ω、・・・)の三角関数の振幅(A2、A3、・・・)が大きい場合、サイン波とは異なる形になり、波形のひずみは大きくなる。
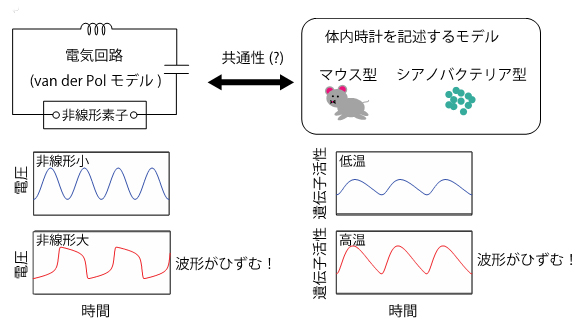
図2 電気回路モデルと生物の体内時計のモデルに見られる波形のひずみの効果の共通性
両者は、解析の対象とする現象も方程式の形も異なるが、波形のひずみ(非線形性が大きいときの電圧と高温のときの遺伝子活性)が周期を長くする点が共通している。
