理化学研究所(理研)開拓研究本部非平衡統計力学理研白眉研究チームの濱崎立資理研白眉研究チームリーダー(数理創造プログラム上級研究員)は、「巨視的な遷移」を伴うような物理的過程において有用となる「速度限界」、すなわち遷移速度に関する不等式を新たに発見しました。 本研究成果は、量子多体系[1]の熱平衡化の時間スケールなどをはじめとする非平衡統計力学[2]へ示唆を与えると同時に、巨視的な量子系の制御など、近年重要となっている量子技術の基礎的な理解に貢献することが期待できます。
ある物理状態が別の物理状態へと遷移するのに要する時間を見積もることは、非平衡統計力学の基本的な問題であると同時に、物理系の状態を操作するために必要なコストの見積もりを与えるという重要性もあります。特に、遷移時間の下限、あるいは遷移速度の上限については昔から研究されており、例えば量子系において、系の全エネルギー揺らぎを用いた速度限界の表式などが知られていました。しかし、巨視的な遷移を含む過程、例えば原子ガスの輸送などでは、既存の速度限界はタイトな(等号達成に近い)不等式を与えてくれませんでした。
今回、濱崎立資理研白眉研究チームリーダーは、こうした巨視的な遷移に関する、定性的に改善された速度限界を導く統一的な枠組みを議論しました。特に、確率の連続の式という物理学の基本原理に基づき、速度限界が「物理量の勾配[3]」と「確率流[4]の大きさ」を用いて表されることを示しました。重要な例として、量子ダイナミクスにこの枠組みを適用した場合には、対応する速度限界が全エネルギー揺らぎではなく、遷移エネルギーを用いた表式によって与えられることを発見しました。
本研究は、オンライン科学雑誌『PRX Quantum』(4月27日付)に掲載されました。
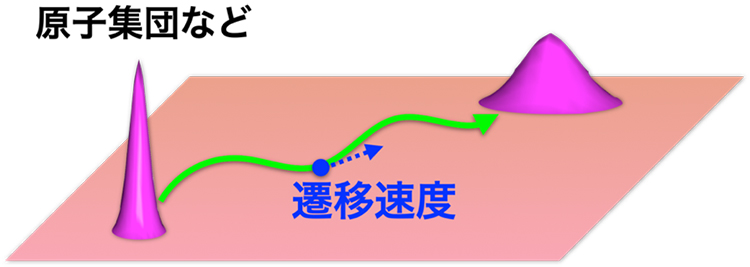
本研究の概念図(原子集団などの巨視的な遷移に対する速度限界の議論)
背景
気体の拡散や電流(電子の流れ)など、自然界の物理現象の多くは動的なものであり、平衡状態[5]にない現象を非平衡現象と呼んでいます。こうした非平衡現象を理解するための理論は完成から程遠く、現代に至るまでさまざまな試みがなされてきました。重要なアプローチの一つは、非平衡過程で成り立つ制約を厳密な不等式の形で見いだしていくことです。
こうした不等式のうち、ある物理状態が別の物理状態へと遷移する時間、あるいは遷移の瞬間的な速度の限界を与える不等式を「速度限界」と呼びます。速度限界に関する先駆的な仕事として、「Mandelstam-Tamm限界[6]」があります。ここで、外界から孤立した量子系において、物理量の量子期待値[7]の瞬間的な時間変化量を単に「物理量の速度」と呼ぶことにします。Mandelstam-Tamm限界によると、物理量の速度の上限は物理量の量子揺らぎ[7]と系の全エネルギー揺らぎの積を用いて表されます。そこから、量子系の状態ベクトル[8]がそのベクトルと直交する状態へ遷移する時間の下限が、全エネルギー揺らぎに反比例することも示せます。Mandelstam-Tamm限界の興味深い点の一つは、速度限界が物理系の状態に依存していることです。すなわち、「全エネルギー揺らぎが小さい状態を考えた場合、必然的に遷移の瞬間速度が小さくなる(遷移時間が大きくなる)」というトレードオフの関係が存在しています。
速度限界は近年盛んに研究されており、その背後に潜んでいる情報論的な理解や幾何学的な理解などが進んでいます。また、孤立量子系だけでなく、古典系や散逸のある量子系などにも速度限界が存在することが分かってきています。さらに、こうした速度限界の応用として、量子断熱時間発展の加速[9]など、系の制御性に対する基本的な理論が導かれることも分かっています。
このように速度限界は非平衡過程の基礎的な理解、また系の制御などの応用などの面でも重要な概念ですが、「巨視的な遷移」があるような場面では問題が起こり得ます。例えば、図1に示したある巨視的に大きな箱の中の隅に閉じ込められた原子の集団が、箱全体に広がっていく過程を考えてみましょう。
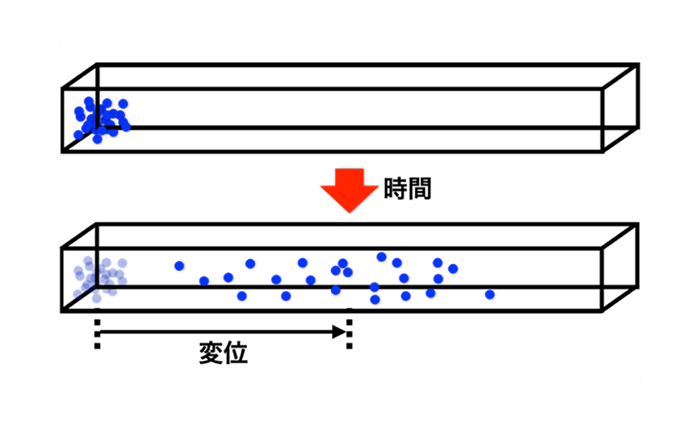
図1 巨視的な遷移の例
例えば、大きな箱(図では一次元方向に伸びている)があり、左端に詰められた粒子集団が広がっていく時の変位を考える。
ここで、原子の平均変位を物理量として取るとします。典型的には、全エネルギー揺らぎは原子数とともに増えていき、時間とともに変位の量子揺らぎも増大していきます。そのため、Mandelstam-Tamm限界、すなわち「物理量の量子期待値の瞬間的な速度」は発散し、「量子状態がそれと直交する状態へ遷移する時間の下限」はゼロに漸近します。一方で、実際には物理量の瞬間速度は有限であるため、遷移時間スケールは箱の大きさにしたがって増えるはずです。つまり、こうした単純な過程ですら、巨視的なスケールの遷移がある場合には、Mandelstam-Tamm限界はタイトな速度限界を与えてくれないのです。
さて、こうした巨視的な量子系での速度に関する有用な不等式として、「Lieb-Robinson限界」が知られています。Lieb-Robinson限界は、局所的に相互作用する量子多体系における情報の伝搬速度の(有限な)上限を与えます。つまり、特殊相対性理論[10]によれば光速が情報の伝搬速度の上限になりますが、非相対論的な量子系でも似た制約が現れることを意味しているわけです。しかし、Lieb-Robinson限界はMandelstam-Tamm限界と異なり、物理系の状態に依存しません。そのため、状態によってはあまりタイトな(等号達成に近い)不等式を与えてくれませんし、「全エネルギー揺らぎと遷移時間のトレードオフ関係」に対応する関係も明確ではありません。このように、Mandelstam-Tamm限界のような物理系の状態に依存し、かつ巨視的な遷移でも有用となる速度限界の一般的な理論はこれまで知られていませんでした。
研究手法と成果
本研究ではまず、「確率の連続の式」に基づき、巨視的な遷移に対して有用な速度限界を導く統一的な枠組みを議論しました。最初に、巨視的な系のダイナミクスを理解するために系を離散的だと仮定し、これをノード(点)とエッジ(線)からなる構造(グラフと呼ばれます)に対応させます(図2)。例えば、量子多体系の場合、ノードはヒルベルト空間[11]の自然な基底を表し、エッジはハミルトニアン[12]によって遷移できるノード同士を結びます。量子的な状態はノード上に定義された波動関数[13]を用いて表され、量子ダイナミクスはその波動関数の変化となります。
ここで、確率の連続の式、すなわち「確率(密度)[4]の減少/増加が確率流(密度)の流出/流入を用いて与えられる」という、物理学の基本法則に注目します。上記のグラフ上に対しては、ノード上の確率分布[4](量子系であれば波動関数の2乗)とエッジ上の確率流に対して連続の式が成立すると期待されます。この連続の式を用いることにより、ノード上で定義された物理量の期待値における瞬間的な速度の上限が、「その物理量のグラフ上の勾配」と「確率流の大きさ」を用いて表されることを示しました。
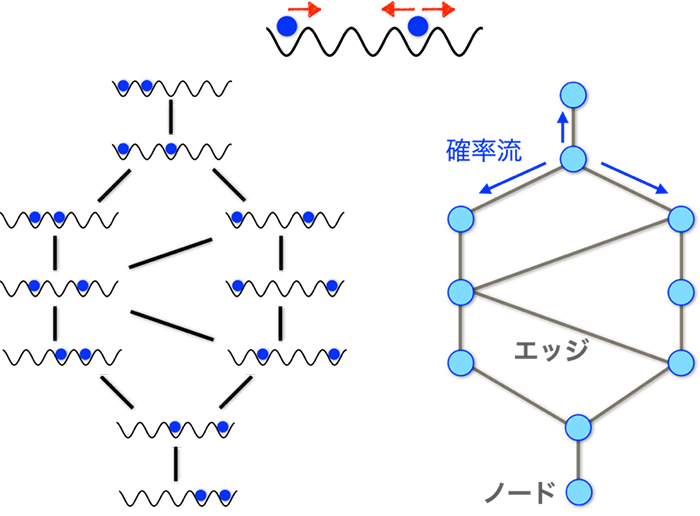
図2 量子系のグラフへの対応への例
ここでは簡単のため、5サイトの箱に2個原子がある場合の運動を考える(一つのサイトには二つ以上原子が入れないとする)。左図のように、系の状態を表す基底は全部で10通りあり、それぞれの状態は原子のホッピングによって遷移できる。これを、状態を表すノードと、その間のエッジとしてグラフに書いたものが右図である。ノード上の確率分布を定義すると、エッジに関して確率流が定義でき、それらの間に連続の式が成立する。
また、重要な点として、物理量そのものやその揺らぎではなく、その勾配が現れるため、物理量期待値の瞬間的な速度の上限が巨視的な遷移に対しても抑制されることを指摘しました。例えば、上で考えた原子集団の場合に平均変位を物理量とすると、平均変位の揺らぎは一般には時間とともに大きくなりますが、その勾配は常に小さいままであることが分かります。なお、ある状態が別の状態へ遷移する時間も同様に議論でき、巨視的な遷移についても有用な(系の大きさとともに増大する)下限を得ることができます。
さて、この枠組みの最も重要な場合として、外界から孤立した量子系の速度限界を議論します。この場合、確率流は量子状態の位相勾配[14]を用いて表されるため、速度限界は「位相勾配が小さい状態を考えた場合、必然的に瞬間速度が小さくなる(遷移時間が大きくなる)」という新しいトレードオフ関係が示唆されます。さらに式変形を行うことで、確率流の大きさが系の遷移エネルギー(ハミルトニアンの遷移部分[15]の量子期待値)の増大により抑えられることが分かりました。まとめると、「物理量期待値の瞬間的な速度の上限が、その物理量のグラフ上の勾配と、系の遷移エネルギーというシンプルな量を用いて表される」ということです。ここで、興味深いのはMandelstam-Tamm限界と異なり、全エネルギーでなく遷移エネルギーだけが出てくる点です。また、今回の枠組みで得られた速度限界は系の遷移エネルギーを通じて系の状態に依存しているため、Lieb-Robinson限界に対応する限界速度よりもタイトな限界を与えます。こうした新しい速度限界の有用性を数値的にも確認しました(図3)。
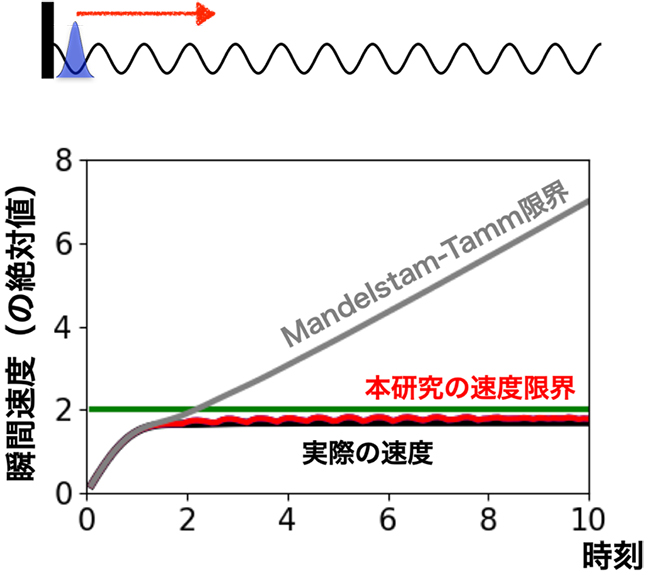
図3 本研究の速度限界の例(1原子の量子ダイナミクス)
(上図)初期状態。広がった一次元系の左端に原子が存在していて、右側に広がっていく。
(下図)各時刻に対する、原子の変位の瞬間速度(の絶対値)。実際の速度(黒線)に対し、本研究の速度限界(赤線および緑線)は時刻とともに増えない上限を与える。特に、赤線の上限は系の状態に依存した良い上限となる。一方、従来の速度限界の一つであるMandelstam-Tamm限界(灰色)は時間とともに発散してしまい、良い上限とならない。
上では物理量の量子期待値を考えましたが、より幅広い設定で巨視的な遷移に対する速度限界も議論することができます。例えば、量子力学の特有の概念である量子コヒーレンス[16]を特徴付ける量に対しても、遷移エネルギーを用いた同様な速度限界を得ることができます。巨視的な系における量子コヒーレンスの理解は量子技術でも重要ですが、この結果は、その量子ダイナミクスに関する一つの厳密な制限を与えるものになっています。また、空間が離散的でなく連続的な場合にも議論ができ、例えば量子気体の速度限界は系の運動エネルギーを用いて表されることが分かります。さらに、確率の連続の式が成立する系では今回の統一的枠組みが適用できるため、古典確率過程や量子確率過程[17]においても巨視的な遷移に有効な速度限界を議論することができます。
今後の期待
本研究は、巨視的な系の遷移に対して特に有用な、非平衡ダイナミクスの厳密な結果を与えています。今後の期待の一つとして、本結果が量子統計力学の基礎的な問題にアプローチする手掛かりになることが考えられます。例えば、非平衡下にある量子多体系は時間とともに平衡状態へと緩和していきますが、それに至る時間スケールの評価は未解決問題の一つです。本研究成果は、こうした緩和の時間スケールに厳密な制約を与えるものと考えられます。
量子多体ダイナミクスの理解は上記のような物理学の基礎理論に関わるのみならず、昨今注目されている量子技術の基盤にも不可欠です。量子技術への期待の高まりの大きな理由の一つが、人工的に実現・制御された量子多体系[18]に関する近年の実験的発展です。本研究の手法・結果がさらに進展することで、こうした量子多体ダイナミクスの制御がどれほど可能かなどの理解に貢献すると期待できます。
補足説明
- 1.
量子多体系
量子力学に従う多数の粒子からなる物理系。 - 2.
非平衡統計力学
統計力学とは、微視的な粒子の集団から、それが集まって発現する巨視的な性質を導くための学問。平衡状態([5]参照)での統計力学は確立されているが、平衡から離れた非平衡状態の統計力学は未完成である。 - 3.
勾配
通常はスカラー場の空間微分により得られるベクトル場であるが、離散的なグラフ上でも同様な概念を定義できる。すなわち、グラフ上の勾配はエッジ(線)でつながれたノード(点)上の物理量の差を用いて表される。 - 4.
確率流、確率密度、確率分布
ランダムに値をとる変数に対し、各々の値をとる確率を表したものを確率分布という。例えばグラフのノード上の確率分布が時間変化する際、その確率の変化を、エッジ上を確率が流れた効果によるものと見なすことができるとき、これを確率流と呼ぶ。また、変数が確率的に連続な値をとる場合、その変数がある値をとる確率は確率密度関数というものにより特徴付けられる。確率流密度は確率密度に対する流れである。 - 5.
平衡状態
巨視的に見て時間変化しないような状態。 - 6.
Mandelstam-Tamm限界
1945年にMandelstamとTammによって提唱された速度限界。ある物理量がユニタリー時間発展により変化する瞬間速度は、系の全エネルギー揺らぎと物理量の揺らぎの積を用いて抑えられることが示された。そこから、量子系の状態ベクトルがそのベクトルと直交する状態へ遷移する時間の下限が、全エネルギー揺らぎに反比例することも示すことができる。 - 7.
量子期待値、量子揺らぎ
量子力学においては、物理量を観測したときの値は測定ごとに揺らぐ。その平均値を量子期待値、標準偏差を量子揺らぎと呼ぶ。 - 8.
状態ベクトル
量子力学に従う系では、その状態は状態ベクトルと呼ばれるベクトルで表される。 - 9.
量子断熱時間発展の加速
量子系をハミルトニアン([12]参照)のパラメータを変化させて制御することを考えるとき、パラメータを無限にゆっくりと動かして得られる状態を断熱状態という。一方、ハミルトニアンに付加項を足すことなどにより、断熱状態を有限の時間で得ようとする研究が近年盛んに行われている。これを断熱時間発展の加速という。 - 10.
特殊相対性理論
1905年にアインシュタインによって確立された力学の理論。物理法則は全ての慣性系において同一であるという特殊相対性原理と、真空中の光速度はどの慣性系でも変わらないという光速度不変の原理を指導原理とする。帰結の一つとして、正の質量を持つ物質は光速度を超えることはできない。 - 11.
ヒルベルト空間
数学的には、内積の定義された完備な複素ベクトル空間のこと。量子力学の状態ベクトルは、ヒルベルト空間におけるベクトルとなる。 - 12.
ハミルトニアン
量子力学に従う系のダイナミクスを定める行列。状態ベクトルの時間変化は、状態ベクトルにハミルトニアン行列をかけたものに比例する。 - 13.
波動関数
状態ベクトルをある基底で展開したときの展開係数。波動関数の絶対値の2乗はその基底に関し、系を測定した場合の確率分布を与える。 - 14.
位相勾配
波動関数は複素数なので、その偏角を考えることができる。これを位相と呼び、空間(あるいはグラフ上ではノード)に関して位相の勾配を考えることができる([3]参照)。 - 15.
ハミルトニアンの遷移部分
ここでは、ハミルトニアンのうち、エッジを通じてノード間を遷移させる項だけを取り出したものを指す。すなわち、ノードに対する基底でハミルトニアン行列を考えたとき、その非対角部分を抜き出したもの。 - 16.
量子コヒーレンス
状態ベクトルは一般にヒルベルト空間の基底の量子的な重ね合わせになっているが、その重ね合わせの度合いを表す。巨視的な量子コヒーレンスの指標はいくつか考えられるが、本研究では巨視的な物理量(相加的物理量)の量子揺らぎを用いて定義された量を考えている。 - 17.
古典確率過程や量子確率過程
確率過程とは、外界からのノイズなどによりランダムに時間変化する事象を、確率変数を用いて定式化したもの。古典確率過程は古典系(量子系ではない系)、量子確率過程は量子系に対する確率過程である。古典確率過程において我々の枠組みを適用すると、最近注目されている熱力学的不確定性関係と呼ばれる不等式の一種が得られる。 - 18.
人工的に実現・制御された量子多体系
原子など、量子力学に従うミクロな自由度の集合を高精度で制御することで作られる系。パラメータの操作性が高く、また観測技術も発展しており、量子非平衡ダイナミクスの実験にも適する。冷却原子系や超伝導キュービット系などが代表的な系である。 - Ryusuke Hamazaki, "Speed Limits for Macroscopic Transitions", PRX Quantum, 10.1103/PRXQuantum.3.020319
原論文情報
発表者
理化学研究所
開拓研究本部 濱崎非平衡量子統計力学理研白眉研究チーム
理研白眉研究チームリーダー 濱崎 立資(はまざき りゅうすけ)
(数理創造プログラム 上級研究員)
 濱崎 立資
濱崎 立資
報道担当
理化学研究所 広報室 報道担当
お問い合わせフォーム
