理化学研究所(理研)数理創造研究センター 数理基礎部門の入谷 亮介 上級研究員、京都大学 大学院農学研究科の辰巳 晋一 准教授らの国際共同研究グループは、空間的な生物多様性の確率分布を推定するための理論を構築しました。本理論は、生物種の在・不在をファジー集合理論[1]の枠組みを用いて表現し、理論物理学で用いられる手法や数学的概念を駆使して解析を行った学際的研究成果です。
本成果は、生息する生物種数の地域間の違いやその増減を定量評価し、生物圏における環境変動が生物多様性に及ぼす影響を予測することに貢献すると期待されます。
生物種数に関する空間的な多様性(ベータ多様性)指数は、その地域差を表す量です。ベータ多様性指数が高いということは、「異なる地域を訪れることで異なる生物種を見つけやすい」ことを意味します。今回、国際共同研究グループは、地域ごとの環境条件の違いを考慮した上で、生物種数のベータ多様性の確率分布を推定するための手法を提案しました。これまでの理論においては、どの生物種がどの地域で見つかるかという確率は、どの地域でもどの生物についても同一であると仮定されていました。本研究ではその理論の一般化に成功し、かつ、複雑な解析を可視化するためのツールと組み合わせて結果を直感的に理解する手法も提案しました。
本研究は、科学雑誌『Ecography』オンライン版(6月4日付)に掲載されました。
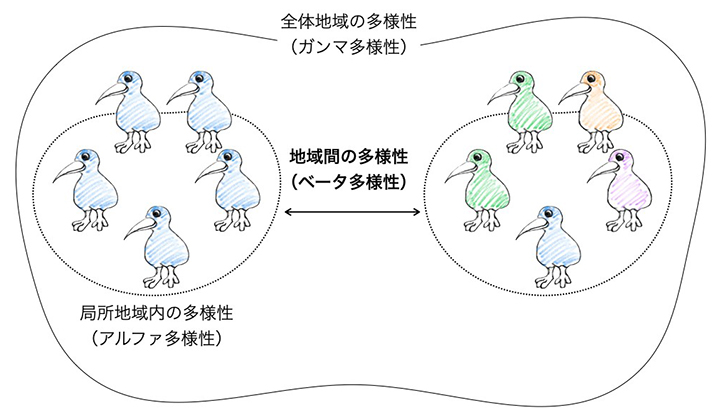
ベータ多様性の概念図
背景
生物多様性とは一般に、どの地域にどのくらいの生物がどのようなバランスで生息しているかを表す概念であり、自然環境の安定的な維持に必要不可欠なものです。生物は、局所地域レベルの多様性(アルファ多様性)から生物圏全体の多様性(ガンマ多様性)に至るまで、いろいろな空間的スケールで生息分布しており、局所地域間の差異を測る生物多様性概念に、ベータ多様性があります。ベータ多様性は、地域ごとにどのくらい異なる生物相が見られるかを表し、複数の空間スケールを結び付ける、重要な概念です(図1A)。しかし、国外外来種・国内外来種の放流、気候変動、環境変動などによって、生物相の均質化(biotic homogenization)が進行しており、ベータ多様性の保全対策が急務となっています。
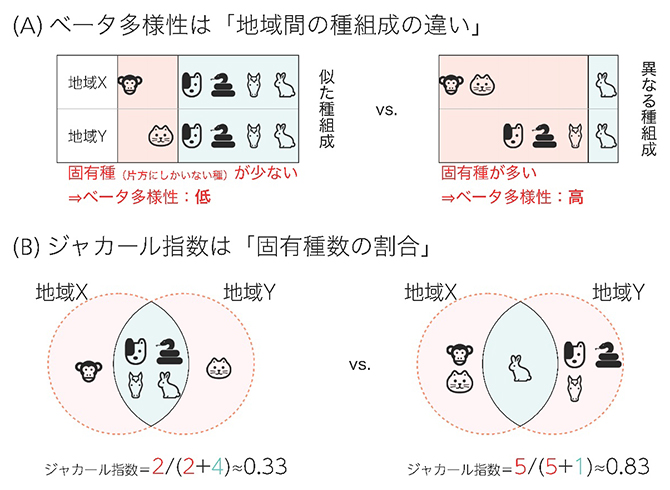
図1 空間的生物多様性(ベータ多様性)の概要
- (A)ベータ多様性は空間的な生物相の違いを表す。ベータ多様性は、地域の固有種が少ないと低く、多いと高い。
- (B)ジャカール非類似度指数(ジャカール指数)は、二つの地域間のベータ多様性を測り、ベータ多様性の指標として用いられる。地域の固有種の割合が高いほど、固有種が多いことを示す。
ベータ多様性の基礎的性質を理解して応用可能性を見いだすには、ベータ多様性の増減に寄与する要素を理解する必要があります。その要素は、環境条件の違いや種の違いとも関わります。生物の生息しやすさの違いとその地域差に関するさまざまなパターンを考慮した理論を構築できれば、その理論に基づいて、高いベータ多様性が実現する法則、いわゆる「ベータ多様性パターン」を予測・説明することが可能になります。
何らかのパターンを予測・説明する際には、数理モデルを用いた理論的アプローチが活躍します。条件から論理的に導かれる帰結や、その起こりやすさを推論できるためです。しかし、先行研究によるベータ多様性パターンには一貫性がありませんでした。特に、環境条件に空間的な異質性がある場合、この問題はより重大です。ベータ多様性が高いのは時・場合(条件)による、という結論しか得られず、結果の一般性や特殊性を推論できません。そのため本当に必要な「パターン」をつかめない状況でした。
研究手法と成果
国際共同研究グループは、生物の空間的な在・不在を確率で表現し、それに基づいてベータ多様性指標の一つであるジャカール非類似度指数(ジャカール指数)[2]の期待値(平均的に期待される値)と分散(期待値からのばらつき)を評価することを考えました。
具体的には、局所群集(異なる生物種の集まった地域)に属する生物種Aが生息している確率(生息確率)を、ファジー集合理論を用いて定義します。例えば、ネコが千葉県に生息している確率(生息確率)をp[千葉,ネコ]=0.7とするなどです。これをあらゆる生物種・地域に対して定義します。これら生息確率値は任意ですから、どの種がどの地域に生息しやすいのかを数理的に表現できます。例えば、p[千葉,ネコ]=0.7、p[東京,ネコ]=0.3、p[千葉,ウマ]=0.3、p[東京,ウマ]=0.6、という状況を考えると、ネコは千葉には生息しやすいが東京には生息しにくく、ウマはその逆、という条件を表現できます(図2A)。
次に、ジャカール指数を考察しました。この指数は、二つの地域の間の生物相の違いを表します(図1B)。各生物・各地域の生物相は、在・不在に関するランダム性(確率性)を持つので、ジャカール指数の確率分布、特に期待値・分散について調べることで、ベータ多様性が取りやすい値やその範囲を調べることができます。
この期待値・分散を、「Schwinger trick(シュウィンガーの固有時間表示)・モーメント母関数[3]」と呼ばれる一連の方法を用いて解析計算で求めました。その結果、これらは「基本対称式」という、変数を入れ替えても値が変わらない、扱いやすい性質を持つ多項式を用いて簡潔に表現でき、さらに、生物学的な解釈も得られることが分かりました。具体的には、その式を用いると、2地域間の共通種の存在がベータ多様性を減らす効果と、確率的にどちらの地域にも生息しにくい種がベータ多様性を増やす効果を分け、それぞれの効果の大きさを推論することができました。
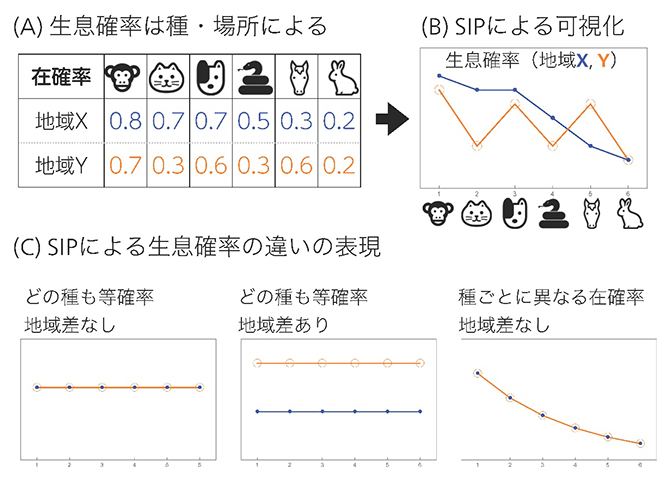
図2 生物の在・不在の変異性とStochastic Incidence Plot(SIP)による図示
- (A)種によって、どの地域に生息しやすいかに違いがある。このような状況の「在」確率を並べるだけでは、多様性指標の性質を推論することが困難になる。
- (B)SIPを用いることで、在・不在の変異性を可視化することができる。
- (C)SIPによって、各種が平等な「在」確率を持ちそれが地域間で「共通である」場合、「異なる」場合や、「地域間に違いはないが種間には違いがある」場合などを可視化できる。横軸は生物種を表す。
続いて国際共同研究グループは、たくさんの生物種の生息確率という複雑な状況を分析するための可視化を考えました。具体的には、各地域の生息確率を、種の名前を横軸としてプロットする、「Stochastic Incidence Plot(SIP)」を提案しました(図2B)。これにより各生物種について地域間の生息確率を容易に比較できます(図2C)。
SIPと数理解析を組み合わせて、国際共同研究グループは二つの主要結果を導きました。一つ目は、「majorization・Schur凸性(シューアとつせい)[4]」という数学的理論を適用したものです。まず、二つの地域のSIPが完全に一致しているという特殊な場合を考えました。このとき、SIPが平らであり全ての種が等しい生息確率を持つときに、ジャカール指数の期待値が最大化されることを証明しました(図3A)。これは、ある一部の種が他の種に比べて高い生息確率を持つ場合には、その種はどちらの地域にも高い確率で生息するため、2地域間の生物相には違いが現れにくいためです。この仮説を「transfer-principle for beta(ベータ多様性に対する移行原理)[5]」と提案しました。なお、本原理が、生物の在・不在が確率的相関を持つ場合にも拡張できることを、補足解析で示しました。
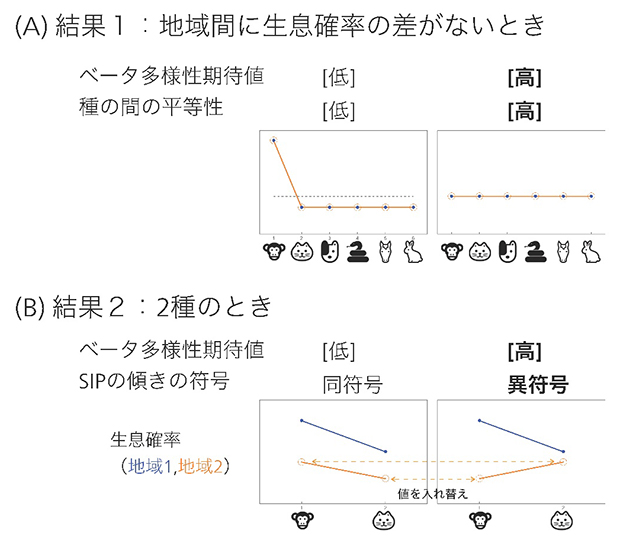
図3 SIPを用いた主要結果
- (A)二つのSIPが完全に同一である、つまり各種が2地域で等しい生息確率を持つ場合。このとき、各種が平等な生息確率を持つ場合が、不平等な生息確率を持つ場合よりも、高いジャカール指数の期待値を持つ。これを「transfer-principle for beta(ベータ多様性に対する移行原理)」と名付けた。数学的には、ジャカール指数の期待値に関するSchur凸性からこの結果が導かれる。
- (B)SIPの傾きが同符号の場合と異符号の場合。異符号のSIPが、高いジャカール指数の期待値を持つ。この例では、左(同符号SIP)では、どちらの地域においても、サルはネコよりも生息確率が高い。つまりサルは共通種である確率が高く、ネコは不在である確率が高い。一方で右(異符号SIP)の場合は、サルもネコも地域1で固有種である確率が高い。
では、二つの地域のSIPが互いに異なる形状を持つ場合はどうでしょうか。SIPとベータ多様性の関係を調べるために、生物種が2である場合を考え、二つ目の主要結果を導きました。そして、任意に生成された四つの確率値を2種・2地域に割り当てる全ての組み合わせを考え、それにより得られる各SIPとジャカール指数の期待値の関係を、数学的な対称性から分析しました。その結果、二つのSIPの傾きが同符号であるときよりも、異符号であるときのほうが、ジャカール指数の期待値が大きいことが分かりました(図3B)。これは、一つ目の主要結果と同様に解釈できます。同符号のSIPでは、特定の種のみが生息する確率が高いのに対し、異符号のSIPでは、ある種はある地域、別の種は別の地域に生息するという「棲(す)み分け」が起こりやすいということです。より一般に、本解析によって、たくさんの種がいる場合でも、2種のSIPの局所的な形状に注目することで、ジャカール指数が大きいパターン・小さいパターンを特定できたことになります。
今後の期待
本研究は、生物分布モデル(species distribution model)と呼ばれる、環境変動効果が生物種分布に及ぼす影響を調べるための数値モデルとも相性が良い理論を提供し、生物種分布の変化を予測するための手助けにもなります。また、ファジー集合理論、Schwinger trickやSchur凸性など、一見すると抽象的な数学が、空間生物多様性の予測や仮説提案に有用であるという点も、学際的な意義を持ちます。本研究から、在・不在だけでなく、個体数や密度などの量的なデータにも同様の結果が当てはまるかどうかや、生物間相互作用の影響があるかどうかなどを調べることが期待されます。
補足説明
- 1.ファジー集合理論
集合理論では、事物x(「元」;例えば実数、ベクトル、生物種など)と、その集まりV(「集合」;実数集合、ベクトル空間、生物群集など)を考え、元xが集合Vに属している、という状態を「x∈V」と表記する。ファジー集合理論では、「x∈Vである確率をp(x, V)とする」と表現することで、集合の性質の確率的な挙動を考察する。本研究では、xを生物種、Vを生物群集、pを生息確率としている。 - 2.ジャカール非類似度指数(ジャカール指数)
集合の非共通部分を全体部分で割り算することによって得られる数学的な量。より一般に、文書間の非類似度、消費者の購買・嗜好傾向の非類似度、化学成分の非類似度などを測るのにも用いられる。 - 3.Schwinger trick(シュウィンガーの固有時間表示)・モーメント母関数
Schwinger trick(シュウィンガーの固有時間表示)は、理論物理、特に量子場理論において使われる計算方法で、分数の数式を、積分の形に変換する。モーメント母関数は、関数のべきを微分に変換する手法。これらを組み合わせると、式の割り算を式の引き算に変換することができるため、計算が容易になることがある。 - 4.majorization・Schur凸性(シューアとつせい)
majorizationとは、量の平等性に関するランク付け(順序)概念。平らなSIP、つまり全ての種が平等な確率で生息する場合が最も高ランクで、特定の種のみが生息する最も不平等な場合が最も低ランク。Schur凸性とは、変数が不平等な場合に高い値、平等な場合に低い値を取る関数の性質を表す。情報理論のシャノンエントロピーの特徴付け、熱力学的平衡状態の遷移可能性、あるいは人文社会科学では、貧富の格差度合いや有効政党数の計算にも用いられる。 - 5.transfer-principle for beta(ベータ多様性に対する移行原理)
transfer-principle(移行原理)は、関数のSchur凸性と関連した概念で、社会において富の配分が偏っていて貧富の格差が大きい状況では、富む者からそうでない者へと富を再配分することが望ましい、という原理。ピグー-ダルトンの原理とも呼ばれ、経済学の基礎的な考え方の一つである。本研究はそれを空間的な生物多様性(ベータ多様性)に用いた。
国際共同研究グループ
理化学研究所 数理創造研究センター 数理基礎部門
上級研究員 入谷 亮介(イリタニ・リョウスケ)
マドリード工科大学(スペイン)応用数学部門
ポスドク研究員 ヴィセンテ・オンティヴェロス(Vicente J Ontiveros)
准教授 ホセ・カピタン(José A Capitán)
スペイン国立研究評議会 ブラナス高等研究所
大陸生態系部門 理論計算生態学グループ
グループ長 ダビド・アロンソ(David Alonso)
リンカーン大学(ニュージーランド)害虫管理保全部門
主任講師 ウィリアム・ガッソー(William Godsoe)
京都大学 大学院 農学研究科
准教授 辰巳 晋一(タツミ・シンイチ)
研究支援
本研究は、日本学術振興会(JSPS)科学研究費助成事業学術変革領域研究(A)「在不在理論の一般化による生物多様性の定量評価(研究代表者:入谷亮介)」による助成を受けて行われました。
原論文情報
- Ryosuke Iritani, Vicente Ontiveros, David Alonso, José A Capitán, William Godsoe, and Shinichi Tatsumi, "Jaccard dissimilarity in stochastic community models based on the species-independence assumption", Ecography, 10.1002/ecog.07737
発表者
理化学研究所
数理創造研究センター 数理基礎部門
上級研究員 入谷 亮介(イリタニ・リョウスケ)
京都大学 大学院 農学研究科
准教授 辰巳 晋一(タツミ・シンイチ)
発表者のコメント
理論生物学では、数理的解析の結果を生物学的に理解して定量化できるかどうかも重要です。本研究は、数理的解析法よりも、結果を理解するための図示や解析法の方が、着想に時間がかかりました。分野の垣根にとらわれることなく数学・物理・社会科学の概念を活用できたこともうれしく思います。(入谷)
 入谷 亮介
入谷 亮介
報道担当
理化学研究所 広報部 報道担当
お問い合わせフォーム
京都大学 広報室 国際広報班
Tel: 075-753-5729
Email: comms@mail2.adm.kyoto-u.ac.jp
