理化学研究所(理研)放射光科学研究センター放射光イメージング利用システム開発チームの加藤健一専任研究員(科学技術振興機構(JST)さきがけ研究者)らの共同研究グループ※は、X線検出器の感度ムラによるノイズに埋もれていた信号を浮き彫りにする「レリーフ補正法」を開発しました。
本研究成果は、さまざまなタイプの検出器にも応用できる高い汎用性を秘めているため、画像検出器を用いた病状の診断精度の向上などにも貢献すると期待できます。
今回、共同研究グループは、原子レベルの構造解析を妨げている一因であるX線検出器の感度ムラを補正する「レリーフ補正法」を開発しました。同法は、観測データに基づき真の感度を統計的に推定するもので、補正前には1%近くあった感度ムラが約0.1%へ10分の1に減少することが分かりました。その結果、これまで感度ムラによるノイズに埋もれて検出困難だった微弱な散乱信号を観測できるようになり、X線構造解析の精度が飛躍的に向上します。
本研究は、英国の科学雑誌『Journal of Synchrotron Radiation』(5月号)の掲載に先立ち、オンライン版(4月5日付け)に掲載されます。
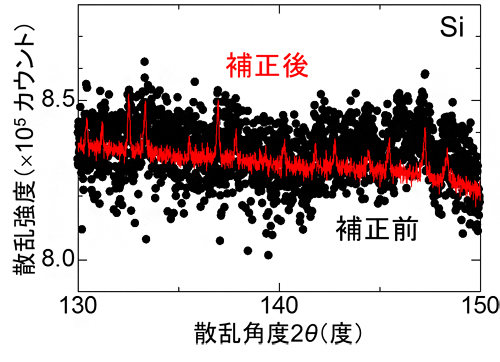
図 レリーフ補正で浮き彫りになったシリコン(Si)結晶からのブラッグ反射
※共同研究グループ
理化学研究所 放射光科学研究センター
放射光イメージング利用システム開発チーム
専任研究員 加藤 健一(かとう けんいち)
(JSTさきがけ研究者)
次世代検出器開発チーム
チームリーダー 初井 宇記(はつい たかき)
兵庫県立大学大学院 物質理学研究科
教授 田中 義人(たなか よしひと)
(理化学研究所 放射光科学研究センター 物理・化学系ビームライン基盤グループ 客員研究員)
九州大学 カーボンニュートラル・エネルギー国際研究所
教授 山内 美穂(やまうち みほ)
(理化学研究所 放射光科学研究センター 可視化物質科学研究グループ 客員研究員(研究当時))
主幹研究員 尾原 幸治(おはら こうじ)
※研究支援
本研究の一部は、JST戦略的創造研究推進事業 チーム型研究(CREST)・個人型研究(さきがけ)複合領域「計測技術と高度情報処理の融合によるインテリジェント計測・解析手法の開発と応用(研究総括:雨宮慶幸、副研究総括:北川源四郎)」のさきがけ研究課題「データ駆動型全散乱計測に基づく不均質現象可視化システムの開発と応用(研究者:加藤健一)」および日本学術振興会(JSPS)科学研究費補助金基盤研究C「放射光全散乱によるナノPdの水素吸蔵非平衡状態における構造可視化(研究代表者:加藤健一)」の支援を受けて行われました。
背景
X線を試料に照射すると、強さも形もさまざまなX線があらゆる方向に散乱されます。それらの散乱X線には、原子の並び方やその乱れに関する情報が含まれているため、広範囲にわたって高いSN比[1]と解像度で検出することが必要です。しかし、そのような要求を満たす仕様のX線検出器を用いるだけでは十分とはいえません。
一般に、検出器には「感度ムラ」と呼ばれる個々の画素のX線に対する感度のばらつきが少なからず存在します。検出器の実質的なダイナミックレンジ[2]は、この感度ムラに大きく左右されます。つまり、検出器の良し悪しは、感度ムラの補正次第といっても過言ではありません。その補正には、あらかじめ強度の分かっているX線を用いるのが一般的でした。
ただし、補正の基準となる値にも誤差があり、それが統計誤差[3]の範囲を超えると使えないため、放射光のような極めて強いX線に対しても有効な感度補正法はこれまで確立されていませんでした。
研究手法と成果
共同研究グループはまず、散乱データをもとに検出器の真の感度を統計的に推定できないかと考えました。ある試料にX線を照射し、一定の角度(Δ2θ)に散乱されるX線を検出器の異なる領域1と2で測定したとします(図1)。測定時間が同じであれば、互いの強度は統計誤差の範囲で一致するはずです。しかし、感度ムラによるノイズが統計誤差を上回ると一致しなくなります。今回開発した方法は、この不一致度を利用して感度を統計的に推定しようとするもので、従来法と異なり、補正のための基準は一切不要です。
感度ムラは、原理的には一度補正すれば済むはずですが、実際には検出器の経年変化や実験環境の変化などが感度に影響を及ぼすため、その都度補正する必要があります。そこで、「観測結果(散乱データ)から見えない状態(真の感度)を推測し明らかにする」というベイズ推定の考え方をもとに、さまざまな試行実験を行いました。その際、散乱データを測定するたびに補正係数を更新することにより、真の感度に近づく速度が向上するのではないかという着想に至りました(図2)。
この方法によると、3日以上かかっていた測定を半日以下に短縮でき、検出器の状態や実験環境に合わせてその都度補正することが可能になりました。さらに、更新の回数や順序を最適化することで、更新しない場合より高い精度で補正できることが分かりました。
この補正法を、大型放射光施設「SPring-8[4]」の理研物質科学ビームラインBL44B2にある全散乱計測システム(図3)に適用しました。その結果、これまで感度ムラによるノイズに埋もれて検出できなかった微弱な散漫散乱[5](図4a)やブラッグ反射[6](図4c)を観測できるようになりました。今回、見えなかったものが「浮き彫り」になったことから、この方法を「レリーフ(Relief)補正法」と名付けました。さらに、補正前でも検出されていたブラッグ反射はより一層鮮明になりました(図4b)。これらの散乱の一部から、補正前はX線強度に対して1%近くあった感度ムラが約0.1%へ減少していることが分かりました(図5)。
今後の期待
今回開発したレリーフ補正法は、画像検出器などさまざまなタイプの検出器にも応用できる高い汎用性を秘めているため、病状の画像診断の信頼性向上などにも貢献すると期待できます。また、計測器の持つ本来の性能を最大限発揮させるものであり、放射光施設のような限られた大型研究基盤の有効活用にもつながると期待できます。
原論文情報
- Kenichi Kato*, Yoshihito Tanaka, Miho Yamauchi, Koji Ohara, and Takaki Hatsui, "A statistical approach to correct X-ray response non-uniformity in microstrip detectors for high-accuracy and high-resolution total-scattering measurements", Journal of Synchrotron Radiation, 10.1107/S1600577519002145
発表者
理化学研究所
放射光科学研究センター 利用システム開発研究部門 物理・化学系ビームライン基盤グループ 放射光イメージング利用システム開発チーム
専任研究員 加藤 健一(かとう けんいち)
(JSTさきがけ研究者)
報道担当
理化学研究所 広報室 報道担当
Tel: 048-467-9272 / Fax: 048-462-4715
お問い合わせフォーム
科学技術振興機構 広報課
Tel: 03-5214-8404 / Fax: 03-5214-8432
E-mail:jstkoho[at]jst.go.jp
産業利用に関するお問い合わせ
JST事業に関すること
科学技術振興機構 戦略研究推進部 グリーンイノベーショングループ
中村 幹(なかむら つよし)
Tel: 03-3512-3525 / Fax: 03-3222-2066
E-mail:presto[at]jst.go.jp
※上記の[at]は@に置き換えてください。
補足説明
- 1.SN比
信号(Signal)とノイズ(Noise)との比。 - 2.ダイナミックレンジ
その機器の扱える最高のSN比。強い信号と同時に弱い信号を測定するには、高いダイナミックレンジが必要とされる。 - 3.統計誤差
個々に予測できない統計的性質を持つ偶然誤差の一種。X線計測の場合は、計数値の平方根に相当する誤差を持つ。 - 4.SPring-8
兵庫県播磨科学公園都市にある世界最高性能の放射光を生み出す大型放射光施設。放射光は、電子を光とほぼ等しい速度まで加速し、磁石によって進行方向を曲げた時に発生する細く強力な電磁波。X線は電磁波の一種で紫外線より波長が短い。 - 5.散漫散乱
ガラスなどの非晶質によるX線などの散乱。方向性は鋭くないが特徴的な方向分布を持つ。結晶でも原子の並び方の乱れなどでも生じる。 - 6.ブラッグ反射
結晶によるX線などの散乱のうち鋭い方向性を持つ回折で生じる。複数の反射の位置や強度から原子の並び方を知ることができる。
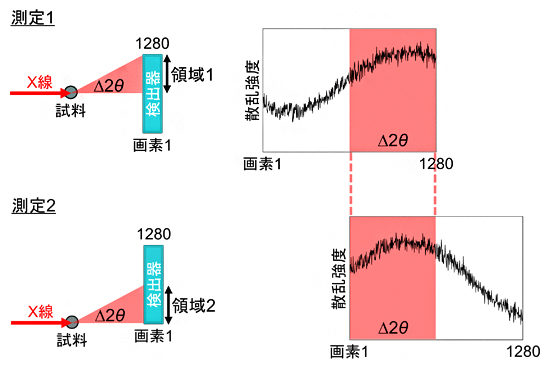
図1 X線感度の統計的推定のための散乱データ測定原理
X線をある試料に照射し、一定の角度Δ2θに散乱されたX線を検出器の領域1と領域2で測定したそれぞれのデータを比較することで、各画素の真の感度を推定する。
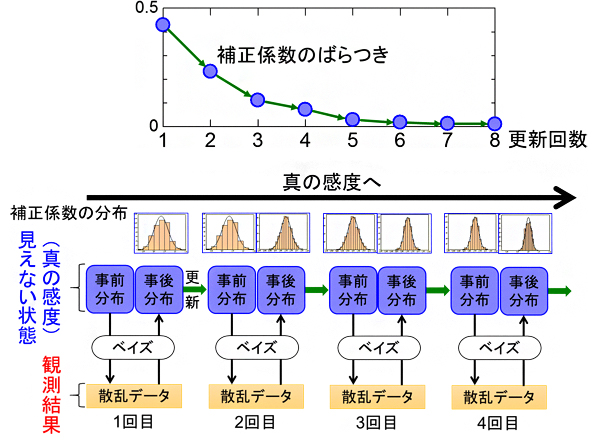
図2 ベイズ推定の繰り返しによる補正係数の変化
観測結果(散乱データ)から見えない状態(真の感度)を推測し明らかにするベイズ推定を繰り返すことで、真の感度へより早く近づくことができる。棒グラフと折れ線グラフはそれぞれ補正係数の分布とばらつきの変化を示しており、推定精度が向上していく様子が分かる。

図3 SPring-8のBL44B2に設置されている全散乱計測システム
DECTRIS社(スイス)製MYTHENというX線検出器が15個、散乱角度の方向に隙間なく並べられている。一度に150度の範囲を0.01度の解像度で散乱データを測定することができる。
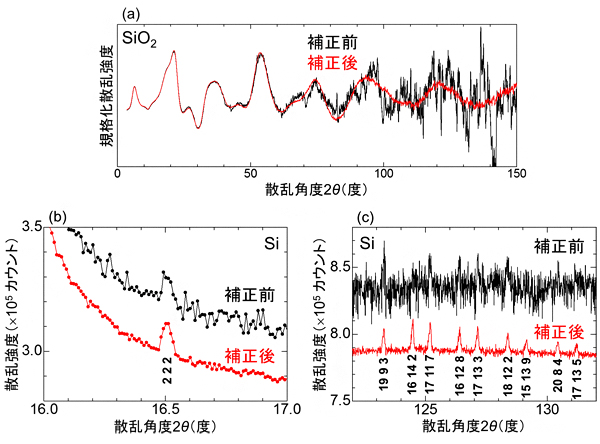
図4 レリーフ補正が散漫散乱(a)とブラッグ反射(b、c)に与える効果
(a)石英(SiO2)ガラスの補正前後の散漫散乱。大きい角度が見やすいように散乱強度を規格化している。(b、c)シリコン(Si)結晶の補正前後のブラッグ反射。重ならないように補正後のデータを下にずらしている。グラフ内の数字はブラッグ反射の代表的な指数。実験に使用したX線の波長は0.45Å。aとcのグラフでは、補正前に検出できなかった微弱な信号が観測できており、bのグラフでは補正前でも検出されていた信号がより鮮明になったことが分かる。
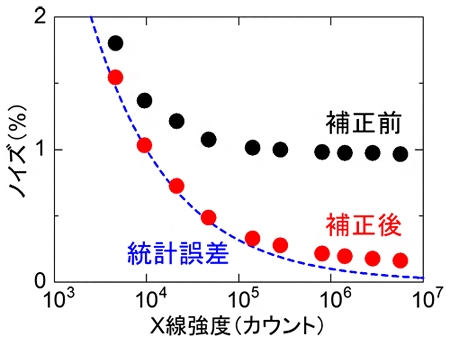
図5 X線強度に対するノイズの割合
石英ガラスの散漫散乱から見積もった補正前後のX線強度に対するノイズの割合。比較のために統計誤差も示している。X線強度が100万(106)カウントあたりのノイズを見ると、補正前は1%近くあるが、補正後は統計誤差を差し引くと、約0.1%へ減少していることが分かる。
