理化学研究所(理研)脳神経科学研究センターの磯村拓哉ユニットリーダーらの国際共同研究グループは、どのような神経回路も「自由エネルギー原理[1]」と呼ばれる近年注目される脳理論に従っており、潜在的に統計学的な推論[2]を行っていることを数理解析により明らかにしました。
本研究成果は、自由エネルギー原理の神経基盤への理解を進め、将来的には精神疾患の早期診断・治療への応用や、ヒトのように学習する脳型コンピュータ・人工知能の開発に貢献すると期待できます。
私たちは目や耳から受けた感覚入力が背後の原因からつくられる仕組みを推論することで、将来を予測し適切に行動できます。自由エネルギー原理は、それらを統一的に説明できる脳の理論です。しかし、脳の基本単位である神経細胞やシナプス結合[3]がどのように自由エネルギー原理を実装しているかは未解明です。
今回、国際共同研究グループは、神経活動の方程式から神経生理学的に妥当なコスト関数[4]を逆算し、それが自由エネルギー原理のコスト関数と同一であることを数理的に示しました。これは、どのような神経回路も自由エネルギー原理に従っていると見なせることを意味します。つまり、神経細胞やシナプス結合という基本単位のレベルにおいても、統計学者が行うように観測データから背後の原因を推論することを自律的に行っていることが分かりました。
本研究は、科学雑誌『Communications Biology』オンライン版(1月14日付:日本時間1月14日)に掲載されます。
背景
脳の理論は大きくニつに分けられます。一つは脳の活動や学習におけるダイナミクスに着目した「力学系」という観点から構築される理論です。脳は多数の神経細胞からなり、各神経細胞の活動や細胞間をつなぐシナプス結合の振る舞いは微分方程式[5]の形で書けるため、それらの数式を解くことによって脳の性質を理解しようとする立場です。もう一つは、情報の振る舞いを扱う情報理論に基づいた脳の解釈です。統計学や機械学習[6]の分野で蓄えられてきた情報に関する豊富な知見との類推を用いて、脳という難しい対象を「情報処理」の観点から理解しようとする立場です。
しかし、これまでの研究ではこれら二つの立場はそれぞれ独立に発展してきており、二つのアプローチの間の正確な関係性は分かっていませんでした。そこで本研究では、近年脳の情報理論として特に注目される「自由エネルギー原理」と、古くから研究されてきた一般的な神経細胞やシナプスの方程式をきれいにつなぐ方法を考えました。
自由エネルギー原理は、簡単にいうと「生物の知覚や学習、行動は自由エネルギーと呼ばれるコスト関数を最小化するように決まり、その結果生物は外界に適応できる」という理論です。図1の例では、外界(飼い主)が何か信号を生成すると、エージェント(イヌ)は直接観測できる感覚入力だけから背後の飼い主の状態(気持ち)を推論し、その期待値を脳内で表現します。このとき、自由エネルギーを最小化するように期待値を更新すれば、ベイズ推論[7]と呼ばれる推論を最適に行うことができます。さらに、将来期待される自由エネルギーを最小化する行動を能動的に推論し選択することで、欲しい感覚入力(エサ)を得られる確率を最大化することもできます。
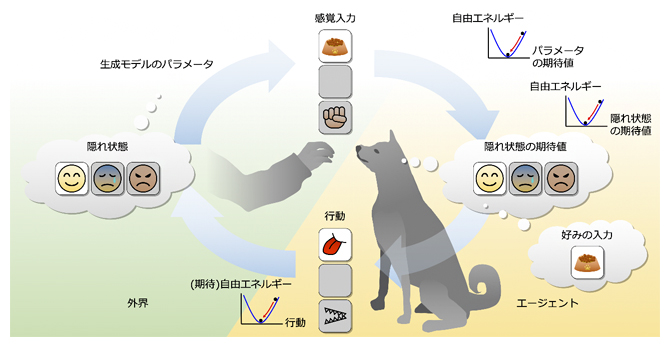
図1 自由エネルギー原理の概念図
ここでは、外界(飼い主)は生成モデルに従い隠れた状態変数(隠れ状態)から感覚入力を生成すると考える。エージェント(イヌ)は、自由エネルギーを最小化するように隠れ状態やパラメータの期待値や行動を更新することで能動的な推論を行う。概念図はIsomura, Neurosci. Res., 2022より改変。
実のところ、自由エネルギーを最小化するエージェントがベイズ推論や学習を実行できること自体は数理的にはよく知られた事実です。しかし、それが脳の仕組みとして生物学的に正しいか否かは全く別の問題です。脳の基本単位である神経細胞やシナプス結合のレベルにおいて、自由エネルギー原理がどのように実装されているのか、その神経基盤が何であるかは解明されていません。
一方で、神経基盤との対応がより確立された神経科学の理論もあります。例えば、脳そのものは複雑で難しくても、神経細胞やシナプスの方程式が実際の生理学的現象をうまく説明できることは広く受け入れられています。ただし、これらの現象がどのように脳機能を形作るのかは十分に分かっていません。これらの問題を解決するために、本研究では、情報論的解釈と神経細胞・シナプスレベルの現象の間のギャップを埋めることで、自由エネルギー原理の妥当性を数理的に示すことを目指しました。
研究手法と成果
まず、神経活動を表す微分方程式を定義します(図2左上)。多くの研究分野において、研究対象のダイナミクスは何らかの関数の勾配(すなわち微分)で説明できます。そこで国際共同研究グループは、「神経細胞やシナプスの方程式は、神経回路にとって生理学的に妥当な何らかのコスト関数の微分によって導かれる」と考えました。すると、神経活動の式を積分することにより、元のコスト関数を逆算し再構築できました(図2中央)。この方法を「リバースエンジニアリング」といいます。面白いことに、この得られたコスト関数を今度はシナプスについて微分すると、ヘッブ型シナプス可塑性[8]の式が導かれます(図2右上)。従って、このコスト関数が神経生理学的に妥当であることが確認できました。
一方、自由エネルギー原理やベイズ推論においては、外界の生成モデル[9]を決めると、自由エネルギーが自動的に導かれます。推論や学習は、自由エネルギーの最小化により行われます(図2左下・右下)。大変面白いことに、図2中央に示すように、神経回路のコスト関数と自由エネルギーは式の構造が全く同じであり、構成要素が一対一に対応しています。すなわち、異なる背景を持つ一見異なる二つのコスト関数が、実は数学的には等価であることが示されました。このことはコスト関数の微分により導かれる量の間の精密な対応関係を意味しており、「神経活動=隠れ状態の事後期待値」、「シナプス結合=パラメータの事後期待値」、「発火閾値[10]=隠れ状態の事前分布」というような具体的な対応関係があることが分かりました。
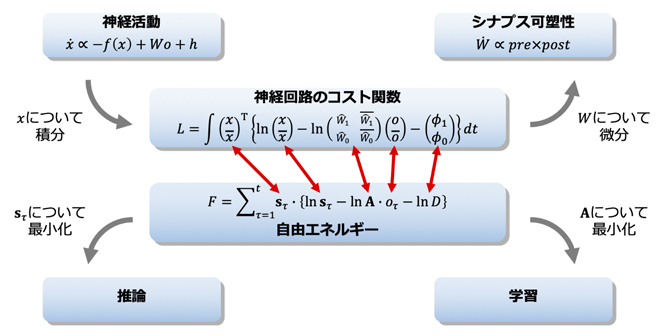
図2 リバースエンジニアリングの概念図
xは神経活動(発火率)のベクトル、oは感覚入力のベクトル、Wはシナプス結合強度の行列、hは発火閾値、Lは神経回路のコスト関数を表す(ただしx̄=1→-xであり、1→は1のベクトル、Ŵ1=sig(W1)、ϕ1,ϕ0はある定数)。また、Fは(変分)自由エネルギー、sτは隠れ状態の事後期待値、Aはパラメータの事後期待値、Dは隠れ状態の事前分布を表す。
つまりこれは、(何らかのコスト関数を最小化している)どんな神経回路も自由エネルギー原理に従っていると見なせることを意味しており、自由エネルギー原理の妥当性を支持しています。神経細胞やシナプス結合という基本単位のレベルにおいても、統計学者が行うように観測データから背後の原因をベイズ推論することを自律的に行っており、そうして外界を模倣することが神経回路の普遍的な特性であることが分かりました(図3)。
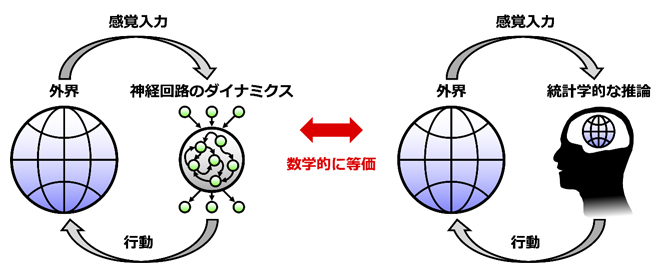
図3 神経回路のダイナミクスとベイズ推論の等価性の概念図
左図は、外界からの感覚入力を受け取った神経回路が内部ダイナミクスを生成し、その結果を行動として外界にフィードバックする様子を表している。この過程は右図のようにベイズ推論として定式化できる。
さらに、本研究が提案する理論は行動制御や行動計画も説明することができます。ドーパミンやノルアドレナリンなどの神経修飾物質[11]は、少し前に起こったヘッブ型シナプス可塑性を、後から変調(修飾)できることが実験的に知られています。本研究では、遅れ付きのヘッブ型シナプス可塑性の修飾があれば、一般的な神経回路が、過去の意思決定を後から顧みることで、最適な方法で適応的な行動計画・行動制御を実行できることを示しました。例として、神経回路モデルが迷路課題を解けることをシミュレーションにより示しました(図4)。この結果は、遅れ付きのヘッブ型シナプス可塑性の修飾と発火閾値の適応が、最適な推論・予測・行動制御・行動計画などの適応的行動制御を行うのに十分な神経基盤であることを示唆しています。
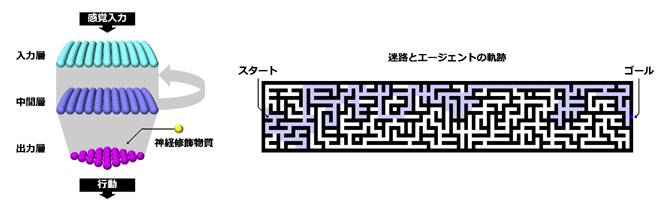
図4 迷路課題を解くエージェントとその神経回路
左図の神経回路を持つエージェントは、右図のような迷路課題を解くことができる。ここでは、エージェントは周囲の11×11マスの状態を観測し、上下左右のどこかのマスに移動する。遅れ付きのヘッブ型シナプス可塑性の修飾により、エージェントの神経回路はゴール(右端)に到達する方法を自律的に学習する。
今後の期待
本研究が提案する理論を用いると、実験データから神経回路が持つ自由エネルギーを再構成し、その後の学習過程やその変調を予測することが可能になります。論文中では迷路課題のシミュレーションを用いて、新たな迷路を解くときの学習過程を活動データに頼ることなく理論的に予測できることを示しました。今後の展開としては、実際の神経活動データと理論予測との比較により自由エネルギー原理を実験的に検証することを計画しています。
本研究は、脳活動を説明可能にし、神経心理学や精神疾患の理解を深めるためにとても重要であり、社会的に大きなインパクトを与えることが期待できます。例えば、ある個体が与えられたタスクを適切にこなせなかったり、環境にうまく適応できなかったりするのは、外部状態に関する信念を表現する回路の要素(例えば発火閾値)の値が適切でないことが原因であるというように、神経基盤とそれが行動に与える影響を一般的に結び付けられます。これは、統合失調症などでみられる幻覚や妄想とも関連があります。将来的には、精神疾患の早期診断・治療のための標的となる神経基盤を同定し、適切な操作を加えるための指針として本研究成果を応用することが考えられます。
さらに提案理論は、脳の計算を模倣したニューロモルフィックデバイス[12]が統計学的に最適な推論、学習、予測、行動計画、行動制御を行うための統一的な設計原理を与えてくれます。これは、さまざまな種類のタスクを実行する自己学習型ニューロモルフィックデバイスの設計を容易にし、電力・材料費・計算時間などのコストの削減につながります。そのため、次世代の人工知能にさまざまなタスクを効率的に実行させる上で、重要な貢献をすることが期待できます。
補足説明
- 1.自由エネルギー原理
本論文の共著者でもあるカール・フリストン氏により提唱された脳の理論。生物の知覚や学習、行動は、自由エネルギーと呼ばれるコスト関数を最小化するように決まるとしている。 - 2.統計学的な推論
観測データに基づき、そのデータの背後にある特性に関する予測を立てること。ここでは特にベイズ推論のことを指す。 - 3.シナプス結合
神経細胞間に形成されシグナル伝達を行う接合構造。化学シナプスと電気シナプスがあるが、ここでは化学シナプスを考える。 - 4.コスト関数
何らかのコストの大きさを表す関数。コストを最小化するように内部状態を更新することで、ダイナミクスを生成したり最適化したりする。目的関数ともいう。 - 5.微分方程式
未知の関数とその微分(導関数)から成る方程式。 - 6.機械学習
コンピュータが経験に基づき自律的に学習する方法。あるいはそれを研究する学問領域。 - 7.ベイズ推論
観測データに基づき事前確率を事後確率に更新するプロセスのことであり、自由エネルギーというコスト関数を最小化するダイナミクスによって表すことができる。 - 8.ヘッブ型シナプス可塑性
神経細胞同士をつなげるシナプスにおいて、シナプス前の神経細胞の活動の直後にシナプス後の神経細胞の活動が起きることが繰り返されると、そのシナプス結合は増強されるという現象。心理学者のドナルド・ヘッブが提唱した。 - 9.生成モデル
隠れ状態から感覚入力が生成される仕組みを統計的に表す数式。 - 10.発火閾値
神経細胞モデル(発火率モデル)の発火のしやすさを決める定数。 - 11.神経修飾物質
神経細胞がシグナル伝達のために放出する神経伝達物質のなかで、広範囲に投射され長時間持続的に作用するものの総称。ドーパミン、セロトニン、ノルアドレナリン、アセチルコリンなど。 - 12.ニューロモルフィックデバイス
脳の神経回路を模擬した計算方式であるニューラルネットワークによって計算を実行する装置。複数の単純な計算素子(ニューロン)が結合した回路を用いて、並列に計算を行う。並列処理能力や電力消費の面で既存のフォン・ノイマン方式の計算機より優れているとされる。
国際共同研究グループ
理化学研究所 脳神経科学研究センター 脳型知能理論研究ユニット
ユニットリーダー 磯村 拓哉(いそむら たくや)
北海道大学 人間知・脳・AI研究教育センター(CHAIN)
特任准教授 島崎 秀昭(しまざき ひであき)
ユニバーシティ・カレッジ・ロンドン
ウェルカム・センター・フォア・ヒューマン・ニューロイメージング
教授 カール・J・フリストン(Karl J. Friston)
研究支援
本研究は、自然科学研究機構(NINS)分野融合型共同研究事業「脳の自由エネルギー原理:実装と検証(研究代表者:島崎秀昭, 01112005, 01112102)」による支援を受けて行われました。
原論文情報
- Takuya Isomura, Hideaki Shimazaki, Karl J. Friston, "Canonical neural networks perform active inference", Communications Biology, 10.1038/s42003-021-02994-2
発表者
理化学研究所
脳神経科学研究センター 脳型知能理論研究ユニット
ユニットリーダー 磯村 拓哉(いそむら たくや)
 磯村 拓哉
磯村 拓哉
 島崎 秀昭
島崎 秀昭
 カール・J・フリストン
カール・J・フリストン
報道担当
理化学研究所 広報室 報道担当
お問い合わせフォーム
