理化学研究所(理研)生命機能科学研究センター 多階層生命動態研究チームの山岸 純平 基礎科学特別研究員と東京科学大学(Science Tokyo)未来社会創成研究院 地球生命研究所(ELSI)の畠山 哲央 特任准教授の共同研究チームは、細胞増殖についてこれまで経験的に知られていた古典的法則の背後にある統一原理を解明しました。これは細胞の増殖・成長が代謝におけるさまざまな資源のやりくりによって制約されるという原理で、一般法則として「大域的制約原理」と名付けました。
本研究成果は、生命科学における基礎理論として細胞増殖のメカニズムへのより深い理解をもたらすだけでなく、発酵産業やバイオ燃料生産といったバイオテクノロジー分野への応用が期待されます。
微生物やがん細胞の増殖速度が栄養源の量にどう依存するかは、生命科学における重要な問題です。モノーの式[1]やリービッヒの最小律[2]といった法則がそれぞれ約80年前と約180年前から経験的に知られてきた一方、多様で複雑な細胞の代謝系からそれらの単純な経験則が現れるメカニズムは長らく謎であり、その普遍性や拡張性には限界がありました。
今回、共同研究チームは、これらの古典的増殖則を再検討し、細胞内代謝[3]における資源分配の帰結として統一的に説明できることを数学的に証明しました。古典的法則を統一する大域的制約原理を解明することで、従来は扱えなかった複数の栄養源の量が変化した際の増殖速度の変化も予測可能になりました。
本研究は、科学雑誌『Proceedings of the National Academy of Sciences(PNAS)』オンライン版(10月3日付)に掲載されました。

「大域的制約原理」の模式図:リービッヒの"段々"樽(たる)
背景
「自己増殖すること」「成長すること」は、生き物にとっての基本的な営みであり、生命を特徴付ける根本的な性質です。この増殖・成長がどのように環境の栄養条件に左右されるのかは、数世紀以上にわたり、生物学の重要なテーマとして研究されてきました。
特に重要な成果として、細菌の増殖速度と栄養濃度の関係を表す「モノーの式」が1940年代に提唱されました。これは、単一の栄養源が増殖速度を決めるというシンプルな法則で、基礎生物学から農学や医学までさまざまな生命科学分野で利用されています。
また、植物の成長の限界が、水や肥料、日光などの資源のうち最も不足しているものにより定められるとする「リービッヒの最小律」という別の法則も、19世紀から知られています。この法則もまた、生態学から農業や発酵産業まで広く応用されてきた経験則の一つです。
このような古典的法則が広く受け入れられ、多くの科学者や技術者の考え方の基盤となってきた一方で、その背後にあるメカニズムは長らく謎に包まれてきました。実際の細胞の増殖は、数千種類にもおよぶ化学反応や化学物質をやりくりして実現されており、単一の資源だけで決まるわけではなく、さまざまな資源や制約が複雑に絡み合っているためです。
今回、共同研究チームは、この古くて大きな課題に挑み、モノーの式とリービッヒの最小律を統一的な枠組みで説明できる包括的理論を確立しようとしました。
研究手法と成果
共同研究チームはまず、これらの古典的増殖則を再検討することで、細胞の増殖速度と栄養条件の関係を表す増殖曲線に現れる性質を整理しました。その結果、栄養が増えると増殖速度も上がるという「単調増加性」と、増殖速度の増加の勢いが徐々に弱まる「凹性(おうせい)(収穫逓減性)」という性質が、増殖曲線において普遍的であることを見いだしました。モノーの式もこれらの性質を満たします。
これらの普遍的性質の背後にあるメカニズムを明らかにするため、細胞内代謝を全体として捉える「資源配分モデル」を構築しました。この数理モデルは既存のシステム生物学・代謝工学の理論的枠組みに基づくもので、取り込んだ栄養源や、それらを代謝する酵素、細胞の体積といった限られた資源を、どの代謝経路にどれだけ割り当てるかを最適化します。その結果、ある栄養源の消費量が増えるにつれて、他の資源の枯渇が新たな制約となっていき、増殖速度の伸びが自然に鈍化することが数学的に証明されました(図1)。この仕組みを「大域的制約原理(Global Constraint Principle)」と名付けました。
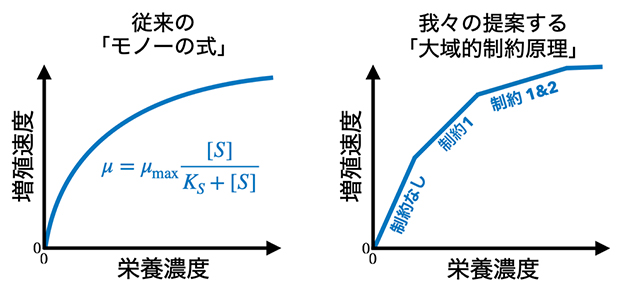
図1 「細胞増殖曲線」の模式図
- 左:従来のモノーの式に基づく細胞増殖曲線。μは増殖速度、μmaxは増殖速度の最大値、Sは栄養濃度、Ksは飽和定数(増殖速度が最大値の2分の1のときの栄養濃度)を表す。栄養濃度が小さいときは分母がKs+S≒Ksとなり増殖速度は栄養濃度Sの1次比例式に近似できるが、栄養濃度が大きくなるとKs+S≒Sとなり増殖速度が最大値に漸近していく。増殖速度の変化は連続的であり、グラフは滑らかな曲線を描く。
- 右:共同研究チームが提案する「大域的制約原理」に基づく細胞増殖曲線。ある栄養源の利用量が増えるにつれて、他の資源の枯渇が新たな制約として加わり、制約がどんどん増えていくために、増殖速度の伸びが段階的に鈍化する。
この原理は、モノーの式などの古典的な増殖則で現れる単調増加性と凹性という二つの性質が、代謝の最適化の結果として普遍的に現れることを示すものです。また、リービッヒの最小律を拡張したものと見なすことができ、古典的な細胞増殖則を統一した理論であるといえます。リービッヒの最小律は、さまざまな栄養源の"板"で囲われた「リービッヒの樽(たる)」の比喩でも表現されますが、新規に提案された大域的制約原理は階段状の板を持つ樽として表現できます(図2)。この「リービッヒの"段々"樽」に水(栄養源)を注いでいくと、水面の高さが初めは一定のペースで増えていきます。しかし新しい資源制約が加わる度に板が階段状に横に広がり、同じ量の水を入れても水位が上がる速度が遅くなります、つまり増殖速度の伸びが抑えられます。

図2 「大域的制約原理」の模式図:リービッヒの"段々"樽
- 左:リービッヒの最小律を説明するための、従来の「リービッヒの樽」。注目する栄養源の消費量が水の量に、その他のさまざまな資源の量が樽板の高さに、水面の高さが細胞増殖速度に相当する。水は一番短い板の高さまでしかたまらない。
- 右:共同研究チームが提案する「大域的制約原理」を説明する「リービッヒの"段々"樽」。栄養源の消費が進み、他の資源の枯渇が制約として加わると、板が階段状に広がって水位が上昇しにくくなる。
さらに、本理論は従来の法則では扱えなかった複数栄養源の複合的な影響も説明・予測できることを示しました。具体例として、炭素源に対する増殖速度の伸びの鈍化が、炭素源以外の酸素源や窒素源などの栄養源の消費量に依存すること、特に酸素源や窒素源が減少するにつれ、炭素源の消費量がより小さい段階で増殖速度の鈍化が起きることを理論的に予測しました。
このような理論的予測は大腸菌の全代謝モデル[4]を用いた数値計算で確認され、また既存の実験結果とも整合的であることが確認されました(図3)。

図3 複数栄養源による細胞増殖の制約:数値計算結果
炭素源の消費量が増えるのに応じて増殖速度は上昇するが、酸素源(左)や窒素源(右)の供給が減少すると、より少ない炭素源消費量で増殖速度の伸びが鈍化し始める。この傾向は大腸菌の全代謝モデルを用いた数値計算で確認され、既存の実験結果とも整合的であることが確認された。mmol/gDW/hは、細胞の乾燥重量1グラムあたりの、1時間あたりのグルコース消費量(ミリモル数)を示す単位
今後の期待
本研究では、モノーの式およびリービッヒの最小律という古典的増殖則を、細胞内資源の配分を最適化するという大域的制約原理の下で統一的に説明し、80年以上にわたる生命科学の謎を解明しました。これにより、これまで経験的に知られてきた細胞増殖速度の普遍的な特性を数理的に理解し、その環境条件の変化に対する応答を予測そして制御するための新たな理論的基盤が整いました。
この新規理論は、発酵産業や食品製造における生産条件の最適化、バイオ燃料や薬剤の生産効率向上など、多くの工業的な分野に数年以内に応用可能であると考えられます。特に、栄養条件を調整して目的の微生物や細胞を高効率に増やす手法は、コスト削減と生産性向上の両立に直結します。
さらに、腸内細菌や、土壌、海洋における環境微生物群集の動態予測にも役立つと期待されます。また、がん細胞や病原菌の増殖特性・代謝特性の理解にもつながり、将来的な治療戦略の新しい指針となる可能性を秘めています。
この研究成果は、生命活動の根幹である細胞増殖に関するより深い理解をもたらし、基礎生物学とバイオ工学・バイオ産業技術の双方における理論的基盤として新しいスタンダードを築くものといえます。
補足説明
- 1.モノーの式
細胞の増殖速度と栄養濃度の関係を示す法則。ノーベル賞受賞者であるフランスの生物学者ジャック・モノーによって1940年代に提唱され、広く受け入れられている。 - 2.リービッヒの最小律
生き物の成長速度の限界は、さまざまな栄養源のうち最も量が少ないもののみで決定されるとする経験則。ドイツの化学者ユストゥス・フォン・リービッヒの1840年の著作により広く知られるようになった。この法則は「リービッヒの樽」と呼ばれるイラストとともにしばしば紹介される。 - 3.代謝
栄養源を分解し、生命活動に必要なさまざまな物質やエネルギーをつくり出す化学反応群。代謝には多くの酵素が関わっている。 - 4.全代謝モデル
生物の全遺伝情報(ゲノム情報)から、その生物がどのような代謝酵素を持つかを推測することができる。この情報を用いて、細胞の全代謝反応を数理モデルで表現したものを全代謝モデル(ゲノムスケール代謝モデル)と呼ぶ。
研究支援
本研究は、理化学研究所運営費交付金(基礎科学特別研究員制度)で実施し、孫正義育英財団や日本学術振興会(JSPS)科学研究費助成事業若手研究「ミクロ経済学と熱・統計力学を用いた代謝システムの解析(研究代表者:畠山哲央、21K15048)」などによる助成を受けて行われました。
原論文情報
- Jumpei F. Yamagishi, Tetsuhiro S. Hatakeyama, "Global constraint principle for microbial growth laws", Proceedings of the National Academy of Sciences(PNAS), 10.1073/pnas.2515031122
発表者
理化学研究所
生命機能科学研究センター 多階層生命動態研究チーム
基礎科学特別研究員 山岸 純平(ヤマギシ・ジュンペイ)
東京科学大学 未来社会創成研究院 地球生命研究所
特任准教授 畠山 哲央(ハタケヤマ・テツヒロ)
Email: hatakeyama@elsi.jp
報道担当
理化学研究所 広報部 報道担当
お問い合わせフォーム
東京科学大学 総務企画部 広報課
Tel: 03-5734-2975
Email: media@adm.isct.ac.jp
