2009年4月30日
独立行政法人 理化学研究所
学校法人 東邦大学
多層状単結晶で世界初の二次元ゼロギャップ電気伝導体を実現
-有機導体α-(BEDT-TTF)2I3で、ゼロギャップ電子系の決定的な証拠を得る-
ポイント
- グラフィンに次ぐゼロギャップ電気伝導体を発見、多層状単結晶では世界初
- 多層状構造の特徴を発見、磁場強度に比例して層間方向の電気伝導度が大きく増大
- FETや熱電材料などの新たな電子機能を持つ分子性デバイス開発に期待
要旨
独立行政法人理化学研究所(野依良治理事長)と学校法人東邦大学(伊藤元博理事長)は、有機導体※1α-(BEDT-TTF)2I3※2が、世界で初めて多層状単結晶で実現したゼロギャップ電気伝導体※3であることを実験的に実証しました。理研基幹研究所加藤分子物性研究室の田嶋尚也専任研究員、加藤礼三主任研究員、東邦大学理学部物理学科の梶田晃示教授らの研究グループによる成果です。
ゼロギャップ電気伝導体は、2005年にグラフィン※4で実現され、大変注目を集めています。これは、素粒子のニュ-トリノ※5と同様、質量ゼロの電子が固体の中に存在し、電気伝導の主役となって、通常の金属や半導体では見られない電気伝導特性や新奇の量子効果を示すためです。一方、研究チームはそれよりも前から、二次元層状構造の有機導体α-(BEDT-TTF)2I3が、金属や半導体と異なるまったく新しいタイプの電気伝導体であることを発見していました。グラフィン実現と同時期に、この物質がゼロギャップ電気伝導体であるという理論が報告されました。この物質をゼロギャップ電気伝導体ととらえると、温度によらず電気抵抗が一定、などの特異な電気的性質や振る舞いを無理なく説明することができます。しかし、本当にゼロギャップ電気伝導体であるという決定的な実験的証拠は、これまで得られていませんでした。
通常、磁場をかけると固体中の電子のエネルギーは、とびとびの値しかとれなくなります。これをランダウ準位※6と呼びます。ゼロギャップ電気伝導体では、ゼロモードと呼ばれる特別なランダウ準位が、エネルギーギャップがゼロの位置に磁場によらず常に現れることが特長です。研究チームは今回、α-(BEDT-TTF)2I3の層間方向の電気抵抗を100mK(ミリケルビン=-272.9℃)という極低温状態の磁場下で調べ、このゼロモードを観測することに成功しました。観測結果は、この有機導体物質が確かにゼロギャップ電子系であることの決定的な証拠となりました。グラフィンは、炭素からなる層構造のグラファイト※4を1層だけにした特殊物質です。一方、α-(BEDT-TTF)2I3は、多層状単結晶でゼロギャップ電気伝導体の特性を示した世界で初めての物質となります。今後、この物質を舞台に、ゼロギャップ電気伝導体における電子の性質を解明し、さらにはFET(電界効果トランジスタ)や熱電材料などの新たな電子機能を持つ分子性デバイスの展開が期待されます。
本研究成果は、米国の科学雑誌『Physical Review Letters』(5月1日号:日本時間5月2日)に掲載されるに先立ち、オンライン版(4月30日付け:日本時間5月1日)に掲載される予定です。
背景
長年、多くの研究者が、運動量空間で伝導帯と価電子帯との間のエネルギーギャップがゼロ、つまり点(コンタクトポイントと呼ぶ)で接しているゼロギャップ電気伝導体を探し求めてきました。例えば、Cd1-xHgxTeという無機物質では、Cd(カドミウム)とHg(水銀)の比率を変えてエネルギーギャップを制御することによって、エネルギーギャップが約6meV(ミリ電子ボルト)まで狭められました(ナローギャップ半導体※3)。しかし、完全なゼロギャップ電気伝導体は見つかっていませんでした。
こうまでして多くの研究者がゼロギャップ電子系を探索する理由は、固体中で電子がとり得るエネルギー状態(バンド構造)が、コンタクトポイント付近では特殊だからです。バンド構造の特殊性によって、電子があたかも質量ゼロの素粒子ニュ-トリノのように固体の中で振る舞い、電気伝導の主役を演じ、通常の金属や半導体では見られない電気伝導特性や新奇の量子効果を示すとされるためです。
2005年には、マンチェスター大学のガイム教授らの研究グループが、層状構造をしているグラファイトを1層だけにしたグラフィンで、ゼロギャップ電子系を実現し、質量ゼロの電子による新奇の量子現象などを発見しました。一方で、このグラフィンの大事件と同時期に、小林晃人特任講師(名古屋大学高等研究院)らの理論グループが、高圧力下にある二次元有機導体α-(BEDT-TTF)2I3(図1)が、理論的にはゼロギャップ電気伝導体の特性を持つことを指摘しました。コンタクトポイント近傍では、2つの円錐型バンドが上下から角突き合わせたゼロギャップ構造(ディラックコ-ン)をしています(図2左)。研究チームの田嶋尚也専任研究員(前東邦大学理学部物理学科)と梶田晃示教授(東邦大学理学部物理学科)らは、2000年より以前から、この物質が1.5ギガパスカルという高圧下で、有機・無機物質含めて今までに例がない、まったく新しい電気伝導体(超ナローギャップ半導体)の挙動を示すことを実験的に見いだしてきました。
高圧下にあるα-(BEDT-TTF)2I3は、室温から1.5Kまでの温度領域で、担体(電気を流す役者:電子や正孔)濃度と易動度(担体の動き易さ)とが反比例して、約6桁ずつ大きく変化しますが、2つの効果が互いに相殺し合って、温度に依存しない電気伝導度を示します。低温では、担体濃度が1015個/cm3程度と低く、106cm2/V.s程度の高易動度の状態にあります。一見、抵抗が温度に依存しないという、不純物の混ざった汚い金属でよく見られる何でもない現象に思えますが、その背景には、これまでになかったまったく新しい現象が起こっていました。このように奇妙な伝導性を示す物質は、高圧下にあるα-(BEDT-TTF)2I3のほかに例がなく、この物質をゼロギャップ電気伝導体ととらえれば、特異な伝導現象は無理なく理解することができます。しかし、「なぜ6桁にも及ぶ担体濃度と易動度の温度変化が、低温に至るまで相殺して、温度に依存しない電気伝導性を示すのか」という疑問は、この物質が本当にゼロギャップ電気伝導体であることを実験的に証明するまで解明することができません。そこで、研究チームは、この物質が本当にゼロギャップ電気伝導体であるという決定的な実験的証拠を得るために、磁場下で現れるゼロギャップ構造に特徴的な電子状態の観測に取り組みました。
研究手法
通常、磁場をかけると、電子のとりうるエネルギーの値がとびとび(ランダウ準位と呼ぶ)になります。ゼロギャップ電気伝導体の場合、そのランダウ準位はさまざまな点でほかの電気伝導体のものとはまったく異なりますが、最も重要な特徴は、コンタクトポイントの位置に特別なランダウ準位(n=0:ゼロモードと呼ぶ)が磁場に依存せず常に現れるという事実です(図2右)。研究チームは、これを調べることで、α-(BEDT-TTF)2I3がゼロギャップ電気伝導体である決定的な証拠を得ようと考えました。
ゼロギャップ電気伝導体に磁場をかけると、この準位は温度に依存せず、磁場強度に比例した数の担体が発生します。二次元面一層当たりの担体濃度は、例えば5テスラの磁場で、1平方センチメートル当たり約1011個(1011個/cm2)ですが、この値は4.2Kの温度(熱)で生じる電流担体の濃度109個/cm2と比較して2桁も大きい値です。このことは、低温状態では、弱い磁場を印加しただけで、熱励起された担体がゼロモードのランダウ電子にとって代わられることを示しています。そこで、研究チームは、層(二次元面)方向に垂直な電流を流した場合に着目しました。この実験では、磁場も層に垂直な方向にかかっているので、電流と磁場の相互作用はなく、直接、担体濃度の磁場変化だけを検出できると考えました。従って、磁場を強くすると、ゼロモードのランダウ電子濃度が増えて、層間方向の電気伝導度が増大すると予想することができます。
研究成果
研究チームは、低磁場でもゼロモードのランダウ電子が支配的となる、十分な低温状態で、層間方向の電気抵抗を調べました。その結果、磁場を強くするとゼロモードのランダウ電子濃度が増大するのを反映して、層間抵抗が磁場強度に反比例して減少する巨大な負の磁気抵抗※7を観測することに成功しました(図3)。例えば、4Kの低温状態で0.2テスラから3テスラまで磁場を変化させると、電気抵抗は約70%も減少します。磁場方位を層に垂直な方向から水平方向に傾けていくと、電気抵抗は単調に増大し続け、二次元伝導面に平行な磁場方位で鋭い極大のピークを示します。この実験結果は、長田俊人準教授(東京大学物性研究所)による理論計算結果と非常によく一致しました(図3)。
さらに、低温・高磁場で、ゼロモードのランダウ電子のエネルギーが磁場で分裂するゼーマン分裂※8を観測することに成功しました。分裂幅(エネルギーギャップ)は磁場に比例して増大するため、分裂幅がゼロモードのエネルギー幅(ランダウ準位は電子散乱などで幅を持つ)よりも十分大きくなる低温・高磁場では、電気抵抗は磁場強度に対して指数関数的に増大することを見いだしました(図4)。
この層間電気抵抗の振る舞いは、磁場下ではゼロモードのランダウ電子が、α-(BEDT-TTF)2I3の伝導性の主役であることを示し、この物質がゼロギャップ電子系であるという決定的な証拠となりました。ゼロギャップ電子系の物質としては、グラフィンが、2005年に新奇の量子ホール効果を示すことが発見されて以来、大変注目されていますが、グラファイトを1層だけにした特殊な構造の物質です。それに対して、α-(BEDT-TTF)2I3は、世界で初めて通常の固体状態である「多層状単結晶」で実現した二次元ゼロギャップ電気伝導体となります。
今後の期待
現在までに、ゼロギャップ電気伝導体と確認できている物質は、グラフィンと今回のα-(BEDT-TTF)2I3だけです。多層状単結晶のゼロギャップ電気伝導体としては、α-(BEDT-TTF)2I3が唯一の物質です。今後、この物質を舞台に、ゼロギャップ電気伝導体の物理が発展していくことになると期待されます。特に、この物質はグラフィンとは異なる特殊なバンド構造(グラフィンとは異なるディラックコーン)をしていることが理論的に指摘され、最近、研究チームはこの事実の実験的な証明を進めています。α-(BEDT-TTF)2I3が、新しいタイプのゼロギャップ電子系の物質である確証が高まると、新奇の電子物性・電子機能の探索が進み、FETや熱電材料などの機能を持つ新しい電子材料、分子デバイスへの開発に期待が持たれます。
発表者
理化学研究所
基幹研究所 加藤分子物性研究室
専任研究員 田嶋 尚也(たじま なおや)
Tel: 048-467-4504 / Fax: 048-462-4661
学校法人東邦大学
理学部物理学科物性物理学教室
教授 梶田 晃示(かじた こうじ)
Tel: 047-472-6990 / Fax: 047-472-6990
報道担当
理化学研究所 広報室 報道担当Tel: 048-467-9272 / Fax: 048-462-4715
補足説明
- 1.有機導体
有機物は、生体、樹脂、化学繊維などのように電気を通さない絶縁体である、というのが常識的な考えであった。しかし、1940年代頃から有機伝導体の開発が行われており、1954年に東京大学理学部の赤松秀雄博士、井口洋夫博士、松永義夫博士らが、ベンゼン環5個からなるペリレン分子と臭素(Br)とを反応させて生じた物質が、高い電気伝導度を持つことを見いだした。1973年には、TCNQ(tetracynoquinodimetance)とTTF(tetrathiafulvalene)という有機分子の間で電子のやり取りをして形成される電荷移動錯体の電子状態が、金属的であることが確認され、金属元素を一切含まない「金属」が誕生した。有機導体の特長は、望みの物性を示すように分子集合体を設計する、いわゆる分子設計あるいは機能設計が可能なことである。多種の有機分子性導体が開発されており、無機物質と同様に絶縁体から超伝導体まで多様な物質群を形成している。 - 2.α-(BEDT-TTF)2I3
有機導体の一つで、有機分子BEDT-TTF(bis(ethylenedithio)tetrathiafulvalene)が並んだ層とI3-イオンが並んだ層とが交互に積層した層状の結晶構造をとる。BEDT-TTF分子2個あたり1個の電子がI3分子に移動し、I3分子は閉殻となるためにI3-イオン層は絶縁層である。一方、BEDT-TTF分子層は電子を放出したことで正孔ができて電気を流す。このようにして二次元電子系が形成されている。ギリシャ文字αはBEDT-TTF分子の配列の仕方を表し、ほかにβ、θ、κ-型などがよく知られている。このような有機導体では、BEDT-TTF分子の配列の仕方が電子物性を決定する。β、θ、κ-型の(BEDT-TTF)2I3は、数Kで超伝導転移するのに対して、α型は135Kで電荷秩序による金属-絶縁体転移を起こす。この絶縁体転移は、1.5ギガパスカル以上の圧力で完全に抑制でき、ゼロギャップ電子系となる。 - 3.ゼロギャップ電気伝導体、ナローギャップ半導体
半導体のうち伝導帯と価電子帯間のエネルギーギャップが狭いものをナローギャップ半導体と呼ぶ。一般にはエネルギーギャップが0~0.5eVの半導体に対して使われている。エネルギーギャップが狭いことが伝導帯と価電子帯の形状を鋭くし、電子または正孔の有効質量は小さくなり、高い易動度を持つことが知られている。このエネルギーギャップがゼロで、伝導帯と価電子帯が点(コンタクトポイント)で接しているものが、ゼロギャップ電気伝導体である。特別な構造をしているために、電子の質量は見かけ上、素粒子のニュ-トリノのようにゼロである。 - 4.グラフィン、グラファイト
グラファイトは炭素から成る元素鉱物で、蜂の巣状の層状物質である。この単一層が最近ゼロギャップ電気伝導体として有名なグラフィンである。一方、グラファイトは層間の相互作用があるために、電子と正孔の小さなフェルミ面を持つ半金属である。 - 5.ニュートリノ
物質を構成している最小単位の物質が素粒子である。ニュートリノは電子の仲間に属する質量ゼロの電気を持たない素粒子である。 - 6.ランダウ準位
磁場中の電子は磁場と垂直な面内でサイクロトロン運動と呼ばれる円運動を行う。量子力学では、このサイクロトロン運動が量子化され、離散的なエネルギー準位に分裂する。これをランダウ準位と呼ぶ。通常の導体では、ランダウ準位は Ћωc(n+1/2) (n=0, 1, 2, …)で表わされる。ここで Ћはプランク定数である。 ωcはサイクロトロン振動数と呼び、磁場 Bと有効質量 m*を用いて ωc= eB/ m*と書ける。一方、ゼロギャップ電子系では、フェルミ速度 vFを使って(2 eЋvF2|n| B)1/2と書けるのが特徴である。従って、n=0の特別なランダウ準位(ゼロモード)が、コンタクトポイントの位置(フェルミエネルギーの位置)に常に存在する。 - 7.磁気抵抗
電気抵抗の磁場による変化を磁気抵抗と呼ぶ。磁場の方向が電流方向と直角な場合を横磁気抵抗、平行な場合を縦磁気抵抗と呼ぶ。通常の電気伝導体では、磁場の方向が電流方向と直角な場合に、磁場と電流が相互作用(ローレンツ力)することによる横磁気抵抗が観測されることが多い。一方、平行な場合にはローレンツ力は働かないので、縦磁気抵抗は観測されないのが普通である。また、磁場によって電気抵抗が増大するときを正の磁気抵抗、減少する場合を負の磁気抵抗と呼ぶ。 - 8.ゼーマン効果、ゼーマン分裂
電子は、スピン磁気量子数の異なる2つの自転状態(上向き、下向き)をとる。磁場がないときは同じエネルギーを持ち縮退しているが、磁場下では縮退が解けて分裂する。これをゼーマン分裂という。分裂エネルギー幅は磁場に比例して増大する。
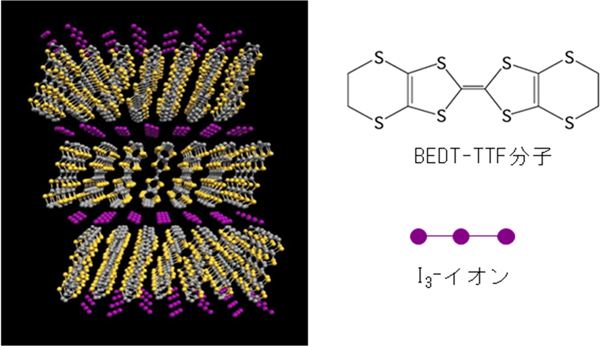
図1 有機導体α-(BEDT-TTF)2I3の結晶構造
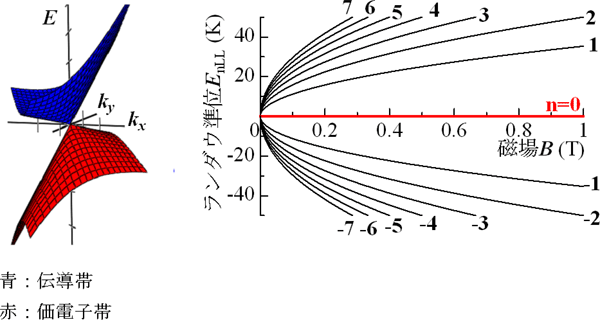
図2 高圧下におけるα-(BEDT-TTF)2I3のゼロギャップ構造(ディラックコーン:左)とランダウ準位(右)
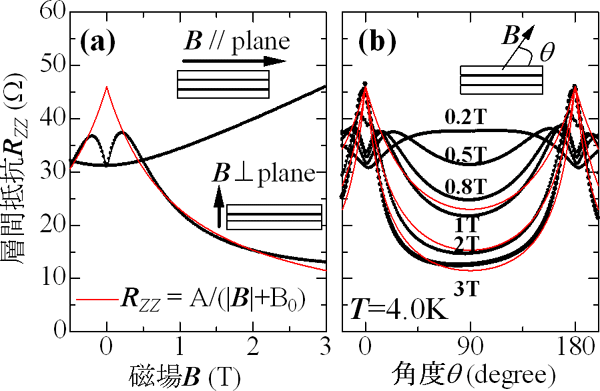
図3 層間抵抗の磁場依存性と角度依存性
磁場方位が層に垂直な場合、層間抵抗の磁場依存性は、0.2テスラ(T)以上の磁場領域で、長田俊人準教授(東大物性研)による理論曲線(赤い曲線)とよく一致し、磁場に比例して電気抵抗が大きく減少する。一方、低磁場領域の不一致は、α-(BEDT-TTF)2I3のディラックコーンが、グラフィンとは異なる構造を持つことに起因することがごく最近明らかになってきた。
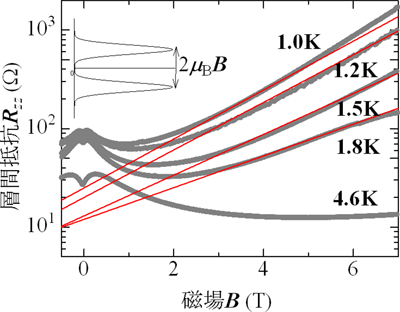
図4 層間抵抗の低温磁場依存性
低温・高磁場で層間抵抗は指数関数で増大する(赤い曲線)。この振る舞いは、ゼロモードのランダウ電子のエネルギーが分裂(ゼーマン分裂)し、分裂幅(エネルギーギャップ)が磁場に比例して増大するためである。
